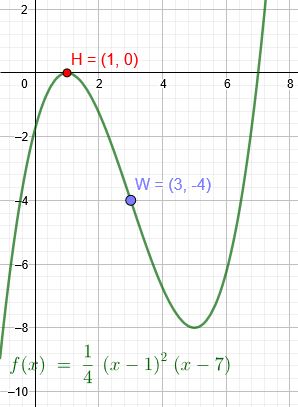
Der Graph einer Polynomfunktion f vom Grad 3 berührt die 1 Achse bei \(x=1\) und besitzt den Wendepunkt W\((3|-4)\) Ermittle die Termdarstellung der Funktion f.
Alternative Lösung:
berührt die 1 Achse bei \(x=1\) Da ist ein Extremwert, darum doppelte Nullstelle:
\(f(x)=a[(x-1)^2(x-N)]\)
\(f'(x)=a[(2x-2)(x-N)+(x-1)^2\cdot 1]\)
\(f''(x)=a[(2x-2N)+(2x-2)\cdot 1+(2x-2)]\)
Wendepunkteigenschaft benutzen: W\((3|....)\):
\(f''(3)=a[(6-2N)+(6-2)+(6-2)]=a[14-2N]=0\)
\(N=7\):
\(f(x)=a[(x-1)^2(x-7)]\)
W\((3|-4)\):
\(f(3)=a[(3-1)^2(3-7)]=a[4\cdot (-4)]=-16a=-4\)
\(a=\frac{1}{4}\):
\(f(x)=\frac{1}{4}(x-1)^2(x-7)\)