Wie viele Millimeter ist der Tropfstein in den ersten 200 Jahren gewachsen? (Integralrechnung am Graphen)

Question

Aufgabe 1:

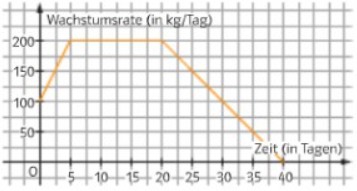
Nebenstehender Graph zeigt die Wachstumsrate eines Tropfsteins in mm pro 100 Jahre in Abhängigkeit von der Zeit \( \mathrm{t} \) (in 100 Jahren).

a) Wie viele Millimeter ist der Tropfstein in den ersten 200 Jahren gewachsen?

b) Wie viele Millimeter wächst der Tropfstein im siebten Jahrhundert?

c) Wie viele Millimeter wächst der Tropfstein in 1000 Jahren?

Aufgabe 2:

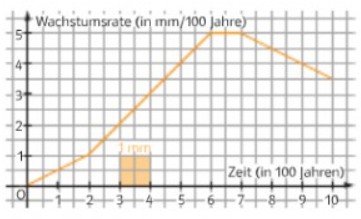
Der Zuwachs von Spargel auf einem Spargelhof entwickelt sich gemäß nebenstehendem Graphen:

Die Ernte beginnt am 20. Tag und geht mit einer konstanten Ernterate von \( 250 \mathrm{~kg} \) pro Tag vonstatten.

a) Berechnen Sie die Spargelmenge, die bis zum Beginn der Ernte gewachsen ist.

b) Welche Gesamtspargelmenge wäre bis zum 40. Tag zu erwarten, falls bis dahin kein Spargel abgeerntet würde?

c) Wie lange dauert die Ernte?

Comments

Für komplexe Anwendungsaufgaben solltest du mal bei den Tutoren von https://www.mathelounge.de/tutors anfragen. Die können das online sehr gut erklären.

Du brauchst hier ja zumindest in den ersten Teilaufgaben immer nur die Fläche unter dem Graphen bestimmen.

Dazu solltest du wissen, wie man die Fläche von Dreiecken, Rechtecken und Trapezen berechnet.

Answer 1

1a) Das entspricht dem Flächeninhalt der Dreiecks mit den Ecken (0/0), (2/0) und (2/1).
Dieser beträgt 0,5*g*h= 0,5*2*1 = 1
und die Einheit ist mm pro 100J * 100J  = mm.
Also ist er um 1mm gewachsen.
b( Das wäre das Rechteck mit den Ecken (6/0)  (7/0) (7/5) (6/5) und dann wie oben.

2a) Fläche des Trapezes über dem Intervall [0;5]
+ Fläche des Rechtecks über [5;20] und dann Einheit kg.