Hängt ein Seil nur unter der Last seines Gewichts, so beschreibt es eine Kettenlinie (Differentialgleichungen, Seillast)

Question

Aufgabe:

Hängt ein Seil nur unter der Last seines Gewichts, so beschreibt es eine Kettenlinie

\( x(t)=b+a \cosh \frac{t+c}{a}, \quad a>0 \)

a) Man rechne nach, dass \( x(t) \) diese Differentialgleichung erfüllt:

\( a x^{\prime \prime}=\sqrt{1+x^{\prime 2}} \)

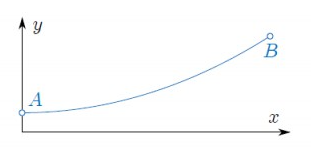
b) Ein Seil soll zwischen den Punkten und \( A=(0 m, 100 m) \) \( B=(300 m, 192.73 m) \) hängen, so dass es in \( A \) horizontal einmündet.

Wie sind \( a, b \) und \( c \) zu wählen?

Hinweis: Die entstehende Gleichung für \( a \) können Sie näherungsweise mit dem Computer lösen.

c) Wie lang muss das Seil aus b) sein?

Answer 1

zu a)

Du leitest die Funktion x(t) 2. Mal ab und setzt die Ableitungen  in die Aufgabe ein.

Dann siehst Du , das die linke Seite = rechten Seite ist.

zu b)

das sind die Anfangswertbedingungen, die Du in die Aufgabe einsetzt.