Die Tragfähigkeit eines Balkens hängt von der Form seines Querschnitts ab.
Die Tragfähigkeit T wird berechnet nach der Formel
T=k*b*h^2, wobei k eine Materialkonstante, b die Breite und h die Höhe des Balkens ist. Für den vorliegenden Eichenstamm gilt k = 1/6.
Ein Balken wird aus einem 30cm dicken Eichenstamm m8it kreisförmigen Querschnitt (Radius r) angefertig. Wie sind die Maße zu wählen, damit seine Tragfähigkeit möglichst groß wird.
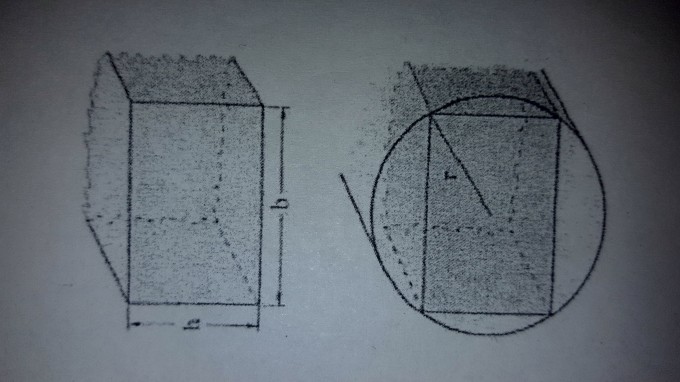
Wie ich die Aufgabe versucht habe:
1) Hauptbedingung: T(b,h) = (1/6) * b * h^2
2) Nebenbedingung: (b^2+h^2)^{1/2} = 30cm | ()^2
b^2 + h^2 = 900 | - b^2
h^2 = 900 - b^2
3) Zielfunktion bilden: T(b) = (1/6) * b * (900 - b^2)
T(b) = (1/6) * 900b - b^3
T(b) = 150b - b^3
4) Extremwerte finden:
T '(b) = -3b^2 + 150 = 0
T ''(b) = -6b
abc-Formel:
b1 = 7,071
b2 = -7,071
T''(7,071) = -6*7,071 = -42,426 (Hochpunkt)
5) Unbekannte bestimmen:
h^2 = 900 - 7,071^2 = 850 | Wurzel
h = 29,155
6) Ergebnis:
T = (1/6) * 7,071 * 29,155^2 = 1001,742
Stimmt das soweit?