Ein Seil hängt zwischen zwei verschieden hohen Masten, die einen Abstand von \( d=100 \mathrm{~m} \) haben. Die Seilkurve habe die Gleichung:
\( y=a \cdot \cosh \left(\frac{x}{a}\right)+b \)
Berechnen Sie: \( b, x_{1}, x_{2} \) und den tiefsten Punkt des Seils.
Daten: \( a=500 \mathrm{~m}, \quad h_{1}=20 \mathrm{~m}, \quad h_{2}=25 \mathrm{~m} \)
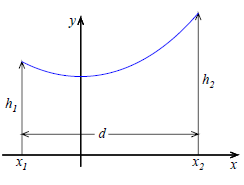
Ansatz/Problem:
Ich habe noch nichts mit solchen Funktionen zu tun gehabt. Es wundert mich daher auch, warum ich diese Aufgabe erhalten habe. Ist mit b die Konstante gemeint? Ist das der Schnittpunkt mit der y-Achse? Kann ich schreiben: y = 500*cosh(x/500) + b? Wie muss ich weiter vorgehen.