f ( x ) = 5/324 * x^2
a ) Berechne die Steigungen des Seils in den
Aufhängepunkten A und B!
f´( x ) = 10 / 324 * x
A : f´( -18 ) = 10 / 324 * -18 =-0.5555
B : f´( 18 ) = 10 / 324 * 18 = 0.5555
b )Berechne das Maß Alpha der Winkel, die
das Seil in den Aufhängepunkten A und B
mit der Horizontalen einschließt.
A = - 29.05 °
B = 29.05
Ich meine das wären oben die Winkel
c)Berechne den Betrag der Zugkraft Z in jeweils einem Aufhängepunkt, wenn das Gewicht des Seils G=500N beträgt. (Das Gewicht verteilt sich je zur Hälfte auf die beiden Aufhängepunkte)
Winkel 90 minus 29.05
Skizze ( anstelle 500 N muß es 250 N heißen )
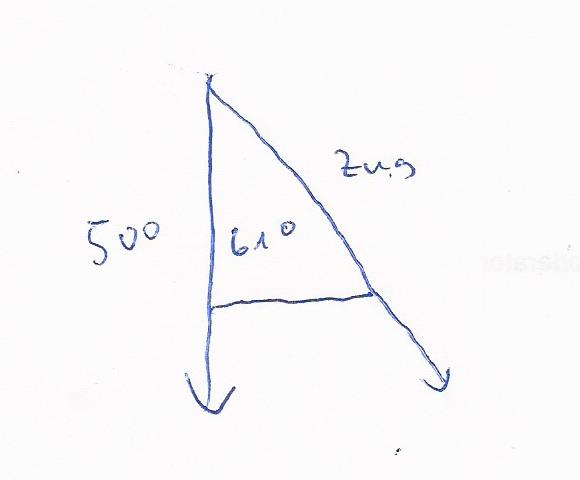
cos ( 61 ) = 250 / Zugkraft