Question

Eine Hochspannungsleitung lässt sich annähernd durch eine Parabel beschreiben. Der Baum ist 50 m vom Mast entfernt und 17,50m hoch.

Auch wenn das Kabel vereist ist und tief durchhängt, hat es noch 5 m Abstand zum Baum.

a) Bestimme eine Funktionsvorschrift für den Verlauf des vereisten Kabels in einem Koordinatensystem deiner Wahl.

b) Wie groß ist der minimale Abstand zum Boden?

c) Bei Sommerhitze dehnt sich das Kabel aus. Der Baum hat nun einen senkrechten Abstand von 16,25 m zum Kabel. Wie groß ist der miinimale Abstand zum Boden dann?

d) Bei normaler Witterung beträgt der Abstand zwischen Baum und Kabel 20m.

Wie viel Luft ist dann unter dem tiefsten Punkt?

Answer 1

hi

wir setzen den nullpunkt des koordinatensystems in die mitte zwischen die beiden mäste.
damit erhält die spitze des rechten masts die koordinaten (100;45)
die leitung 5m über dem baum hat die koordinaten (50|22,5)

dann gehen wir von der gleichung einer nach oben verschobener normalparabel aus:
y = a*x² + b

wir können die beiden koordinaten in die gleichung einsetzen und erhalten
zwei gleichungen mit den beiden unbekannten a, b.

45 = a*100²+b
22,5 = a*50²+b

damit kannst du a, b berechnen und bekommst so deine funktionsvorschrift.
den minimalen abstand zum boden bekommst du, indem du in der
funktionsvorschrift x = 0 setzt.

c)  und d) funktionieren prizipiell genau so.

Comments

wie mach ich das mit dem additionsverfahren und mit welcher funktion muss ich arbeiten

---

du kannst auch das einsetzverfahren wählen, oder etwas anderes.

die funktion ist in der aufgabenstellung vorgegeben, es soll eine parabel sein.

---

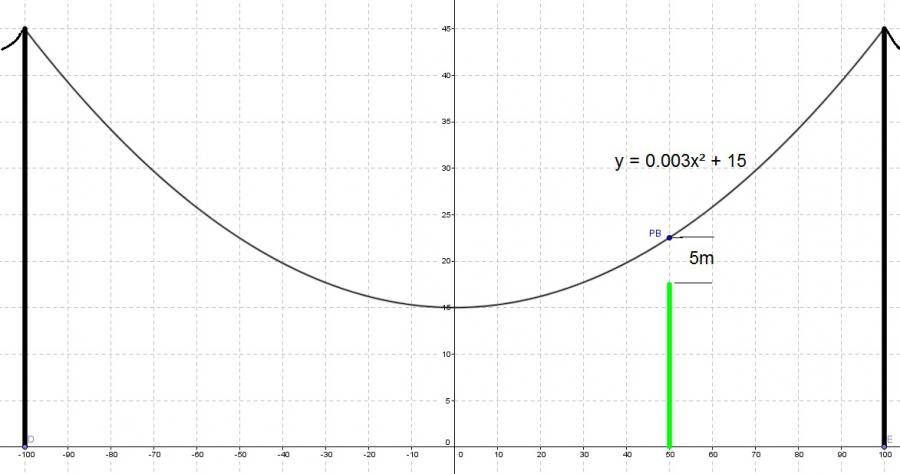
die parabel soll durch die punkte A = (100;45) und B = (50|22,5)
verlaufen.

wir können für jeden punkt eine gleichung schreiben:

1) a*100^2 + b = 45
2) a*50^2 + b = 22,5

damit haben wir zwei gleichungen und zwei unbekannte, die
sich berechnen lassen, z.b. mit dem einsetzverfahren:

1) nach b umstellen b = 45 - a*100²
einsetzen in 2)

a*50^2 + 45 - a*100^2 = 22,5

a(50^2-100^2) = -22,5
a = -22,5/(50^2-100^2) = -22,5/-7500
a = 0,003

b = 45 - a*100^2 = 45 - 0,003 * 10000 = 15

damit bekommen wir die funktionsvorschrift

a)
y = f(x) = ax^2+b = 0,003*x^2+15

b)

der minimale abstand zum boden lässt sich direkt aus der gleichung ablesen:

h_min = 15

c) und d) kannst du nach diesem schema lösen, es ändert sich jeweils lediglich

der punkt B.

lg

---

wieso gibt es nicht c?

---

das ist der gleiche rechenweg wie der erste teil der aufgabe. statt 5m sind es jetzt 16,25m.

es ändern sich nur die koordinaten des kabels über der baumspitze. den rest kannst du 1:1 übernehmen.

---

ok aber mit welcher funktion hast du gearbeitet?

weil ich möchte das nur mit dem additionsverfahren lösen

---

die funktionen stehen doch oben.

ich habe die funktion y = a*x² + b benutzt und jeweils die koordinaten (100;45) und (50|22,5) eingesetzt.

das ergibt die beiden gleichungen

45 = a*100²+b
22,5 = a*50²+b

um a und b zu berechnen, kannst du gern auch das additionsverfahren benutzen.

---

mein lehrer meinte heute aber ich muss diese funktion anwenden f(x)=a*x²+b*x+c

---

okay.

f(x) = ax² + bx + c

b = 0

f(x) = ax²  + c

45 = a*100² + c
22,5 = a*50² + c

jetzt heißt die unbekannte eben c statt b, ansonsten ändert sich an der rechnung  nichts.

---

ja er meinte (0/45)     (200/45)        (50/22,5)