 Aufgabe:
Aufgabe:
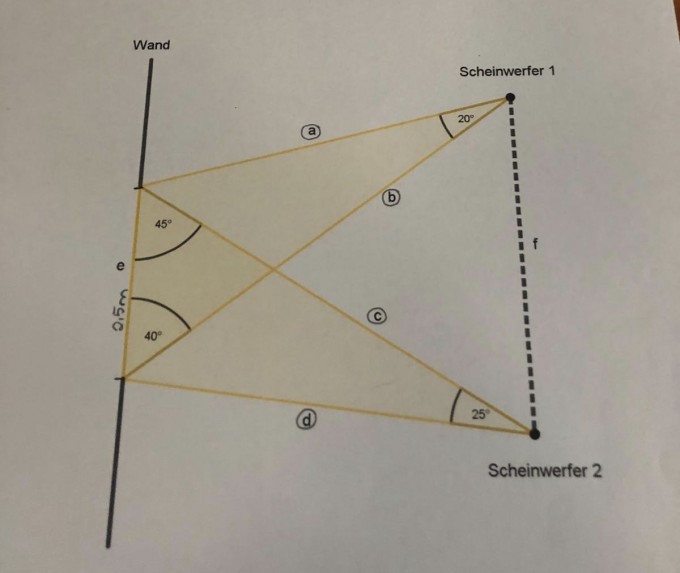
Zwei Scheinwerfer wurden so ausgerichtet, dass sie einen 2,5 m (e) hohen Teil einer Wand beleuchten.
Die Öffnungswinkel der beiden Lichtkegel betragen 20° bzw. 25°. Die inneren Lichtstahlen (b; c) treffen unter einem Einfallswinkel von 40° bzw. 45° auf die Wand.
a) Berechne die Länge der Ränder beider Lichtkegel (b, c, d)
b) Wie groß ist die in der Skizze dargestellte doppelt beleuchtete Fläche?
c) Wie weit sind die beiden Scheinwerfer von einander entfernt?
d) Die Scheinwerfer haben den gleichen Abstand zur Wand. Berechne diese Entfernung.
Problem/Ansatz:
Ich weiß nicht wie ich bei diesen Aufgaben vorgehen muss.
°