Aufgabe:
Berechne die fehlenden Seitenlängen des Dreiecks mit \( a=8 \mathrm{~cm}, \alpha=50^{\circ}, \gamma=90^{\circ} \).
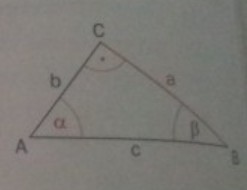
Ausführung: Fertige eine Skizze an und löse die Aufgabe z.B. so:
\( \sin \alpha=\frac{\text { Gegenkathete }}{\text { Hypotenuse }}=\frac{a}{c} \Rightarrow c=\frac{a}{\sin \alpha} \Rightarrow c \approx 10,4 \)
\( c^{2}=a^{2}+b^{2} \Rightarrow b=\sqrt{c^{2}-a^{2}} \Rightarrow b \approx 6,7 \)
Ergebnis: \( b \approx 6,7 \mathrm{~cm}, c \approx 10,4 \mathrm{~cm} \)
Ansatz/Problem:
Ich kann den Schritt c= a/ sin alpha nicht nachvollziehen, wie bekomme ich einen sin alpha Wert, wenn ich den Wert der Hypotenuse nicht kenne?