Geometrie, zwei parallele Strecken, Beweis

Question

Ich bekam eine Aufgabe, wo dieses Fünfeck beschrieben wird:

Ich habe es mit Geogebra erstellt, um es bildlich darzustellen.

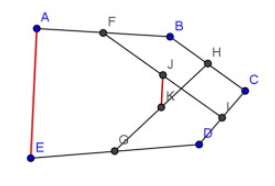
Ich soll beweisen, dass die beiden rot makierten Strecken parallel sind.

Die blauen Punkte sind die Ecken des Fünfecks, und die schwarzen Punkte sind immer Mittelpunkte.

Wenn ihr möchtet, kann ich dieses Fünfeck auch anders darstellen, aber diese beiden roten Strecken sind irgendwie immer parallel, egal wie ich es dreh und bewege.

Ich bekam noch den Hinweis, dass diese Aufgabe sehr gut analytisch (also mit Rechnung) beweisen lässt. Man kann es aber auch geometrisch beweisen.

Answer 1

Man möge sich über den Buchstaben die Vektorpfeile dazudenken:

$$F= \frac{A+B}2 $$$$H= \frac{B+C}2 $$$$I= \frac{C+D}2 $$$$G= \frac{D+E}2 $$$$J= \frac{F+I}2 $$$$K= \frac{G+H}2 $$zu beweisen:$$A-E = \lambda \cdot (J-K)$$
---
$$K= \frac{G+H}2 $$$$K= \frac{ \frac{D+E}2+\frac{B+C}2}2 $$$$K= \frac{B+C+D+E}4 $$
$$J= \frac{F+I}2 $$$$J= \frac{\frac{A+B}2+\frac{C+D}2 }2 $$$$J= \frac{A+B+C+D}4 $$
---
$$A-E = \lambda \cdot (J-K)$$
$$A-E = \lambda \cdot (\frac{A+B+C+D}4-\frac{B+C+D+E}4)$$
$$A-E = \lambda \cdot (\frac{A}4-\frac{E}4)$$

q.e.d.

Comments

dankeee!!! sozusagen ist das Verhältnis der beiden Strecken 1 : 4. nochmals dankeschön!

---

die Buchstaben alle sind Ortsvektoren, oder? also vom Koordinantenursprung

---

Davon bin ich mal der Einfachheit halber ausgegangen, also dass die Koordinaten der Punkte direkt in den Vektor übernommen werden, also vom Ursprung des Systems aus betrachtet.

Und es passt ja, oder?

---

danke :)