Ich kann die Schnittpunkte mit der x-Achse bestimmen, von welcher auch zufällig einer der Schnittpunkt der Kurve mit sich selbst darstellt.
$$x(t)=t^{ 2 }+2\\ y(t)=t^{ 3 }-t\\ \\ Schritt\quad 1\\ y(t)=0=t^{ 3 }-t\\ { t }_{ 1 }=0\\ { t }_{ 2 }=1\\ \\ Schritt\quad 2\\ x(t={ t }_{ 1 })=2\\ x(t={ t }_{ 2\\ })=3$$
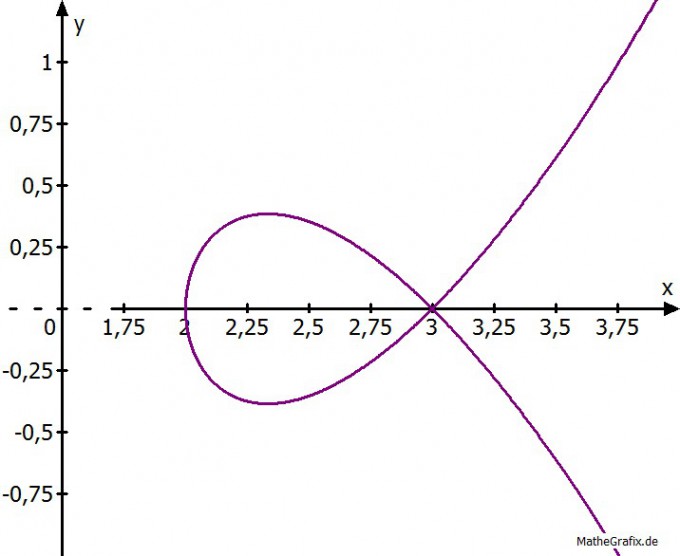
Wie bestimme ich aber den Schnittpunkt der Kurve mit sich selbst allgemein?