Hallo nochmal
Wenn ich dich richtig verstanden habe, dann ist Dein Problem nicht das bestimmen von Ableitungen, sondern zu verstehen warum Du gerade die erste oder zweite Ableitung bilden sollst, abhängig von der Aufgabenstellung.
Meiner Meinung nach ist der Schlüssel die Aufgabenstellung in mathematische Operationen umzusetzen, diemathematischen Operationen richtig zu interpretieren.
Die Aufgabenstellung lautet ja: Die Flughöhe eines Segelflugzeugs in einer zweistündigen Flugphase wird durch die Funktion h(t)=1/1000 (t3-180t2+6000t)+400 modelliert (t in Minuten, h (t) in Metern). Zu welchem Zeitpunkt hat das Flugzeug den größten Höhenverlust?
Nun schau Dir die erste Kurve an. Im ersten blauen Bereich (das sind die ersten 20 min) gewinnt das Flugzeug an Höhe; es steigt von 400m auf 456m.
Jetzt schau bitte auf die zweite Kurve darunter. Diese beschreibt die Steig (blau)- und Sinkgeschwindigkeit (rot). In den ersten 20 min hat die Kurve Werte die über 0 liegen. Die Geschwindigkeit ist also positiv, zeigt an, dass das Flugzeug steigt. Ein kurzer Blick auf die Höhenkurve bestätigt das auch. In dem Bereich in dem die Geschwindigkeitskurve positiv ist, gewinnt das Flugzeug an Höhe.
So wie das Flugzeug im blauen Bereich an Höhe gewinnt verliert es im roten Bereich an Höhe - h(t) nimmt in diesem Bereich ab. Unsere Vermutung, die Geschwindigkeitskurve sollte hier negative Werte haben. Ein Blick auf h'(t) bestätigt das.
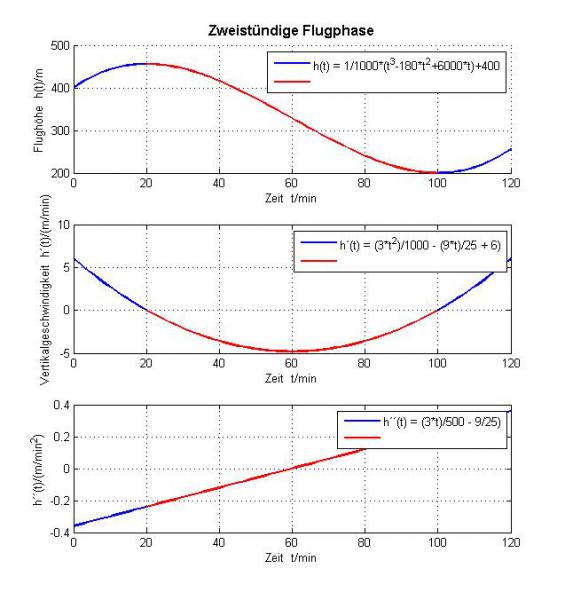
Nun ist der Zeitpunkt gesucht, an dem der Höhenverlust am größten ist. Ganz intuitiv würde ich sagen ist das der Punkt, an dem die Höhenkurve die größte negative Steigung hat, also bei t = 60min. (Falls Dir das nicht ganz einleuchtet habe ich am Ende noch etwas angefügt um das zu erklären.)
Nun ist also ein mathematisches Werkzeug gesucht mit dessen Hilfe Du den t-Wert finden kannst, an dem die Steigung der Höhenkurve die größte negative Steigung hat.
Wie Du schon weißt gibt die Steigung der Höhenkurve die Vertikalgeschwindigkeit an (die ich auch als Steig- und Sinkgeschwindigkeit bezeichnet habe). Die Steigung aber lässt sich mit Hilfe der Ableitung berechnen. Folglich bildest Du die erste Ableitung der Höhenkurve h(t) und erhältst h'(t) das ich mal als s(t) bezeichnen möchte, also h'(t) = s(t). Jetzt hast Du eine Funktion s(t), die die Steigung respektive Vertikalgeschwindigkeit in Abhängigkeit von der Zeit beschreibt. Nun willst Du aber nicht irgendeine Steigung bei irgendeinem t-Wert, sondern den t-Wert mit der größten Steigung.
Wie findet man bei einer Kurve die Extrempunkte? Richtig. 1. Ableitung bilden und 0 setzen. Bevor Du das machst schaust Du noch mal Kurz auf die zweite Kurve. Es handelt sich um eine Parabel und wie unschwer zu erkennen ist, befindet sich der größte negative Wert bei t=60min (oder zumindest ungefähr; genaue Werte aus einem Diagramm abzulesen ist so eine Sache ...).
Nun bilde die erste Ableitung von s(t) --> s'(t). s(t) = h'(t) damit ist s'(t) = h''(t) und setze s'(t) = 0. Als Ergebnis erhältst Du tatsächlich t = 60 min.
Wenn Du s'(t) = 0 bestimmst, dann kennst Du die Extremwerte von s(t), dies sind zugleich die Wendepunkte von h(t) da ja s'(t) = h''(t).
Zusammengefasst: Gesucht ist der größte Höhenverlust = größte Sinkgeschwindigkeit. Die Geschwindigkeit ist da am größten wo die Wegkurve die größte Steigung hat. Den t-Wert der größten Steigung findet man indem man die 2. Ableitung der Wegkurve bildet und 0 setzt.
Jetzt musst Du nur noch prüfen ob es sich tatsächlich um einen Wendepunkt handelt. Da h'''(t) > 0 ist, handelt es sich auch um einen Wendepunkt bzw. um ein Minimum der Geschwindigkeitskurve.
Anhang:
Erklärung warum die größte Sinkgeschwindigkeit auch bei einem t-Wert zu suchen ist, an dem die Steigung am größten ist.
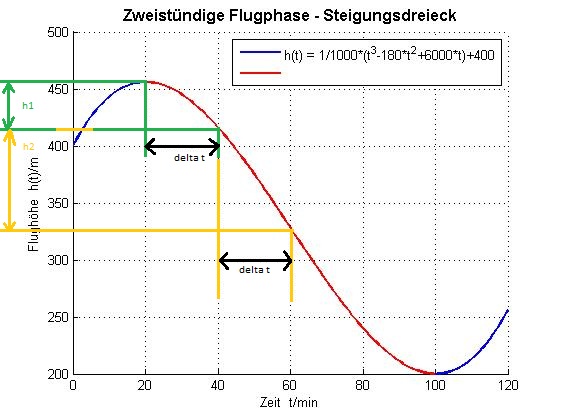
Betrachte zwei gleichgroße Zeitbereiche nur bei unterschiedlicher Steigung. Beim grünen Bereich ist die Steiung geringer also auch die Sinkgeschwindigkeit. Das heißt bei gleicher Zeit delta t ist der zurückgelegte Weg h1 kleiner als bei größerer Geschwindigkeit bzw. Steigung h2.
lg JR