Hallo,
\(K(x)=0,001x^3-0,9x^2+150x+72000\)
a) Zeichnen Sie den Graphen der Funktion K
Das könnte so aussehen:
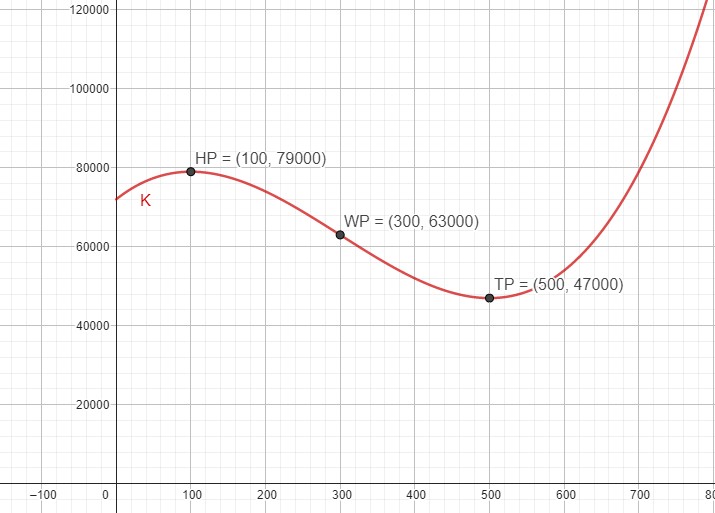
b) Wie hoch sind die Kosten für eine Uhr bei einer Produktion von 500 Uhren pro Tag?
Setze 500 für x in die Gleichung ein und berechne K(x).
c) Untersuchen Sie die Funktion K auf Extrema
Bilde die 1. Ableitung, setze sie = 0 und löse nach x auf. Bestimme dann mit Hilfe der 2. Ableitung, ob es sich um Hoch- oder Tiefpunkte handelt. Setze deine Ergebnisse für x in die Ausgangsgleichung ein, um die y-Koordinaten der Extrempunkte zu bestimmen.
d) Bestimmen Sie den Wendepunkt von K
Bilde die 2. Ableitung, setze sie = 0 und löse nach x auf. Prüfe, ob \(f'''(x)\neq 0\). Um die y-Koordinate zu bestimmen, s. Exrema.
Gruß, Silvia