1. Berechnen Sie die Position des Kohlenstoffatoms:
\( \vec{s}=\frac{m_{H}\left(\begin{array}{c}{1} \\ {1} \\ {1}\end{array}\right)+m_{H}\left(\begin{array}{c}{-1} \\ {-1} \\ {1}\end{array}\right)+m_{H}\left(\begin{array}{c}{1} \\ {-1} \\ {-1}\end{array}\right)+m_{H}\left(\begin{array}{c}{-1} \\ {1} \\ {-1}\end{array}\right)}{m_{H}+m_{H}+m_{H}+m_{H}} \)
\(= \dfrac{ m_{H}\left(\begin{array}{c}{1-1+1+1} \\ {1-1-1+1} \\ {1+1-1-1}\end{array}\right) }{ 4·m_H } \)
\( = \dfrac{1}{4}\left(\begin{array}{c}{0} \\ {0} \\ {0}\end{array}\right)=\overrightarrow{0} \)
Das C-Atom befindet sich also im Ursprung des Koordinatensystems.
2. Berechnen Sie den Abstand des C-Atoms zu den H-Atomen sowie den Abstand zwischen je zwei H- Atomen:
Der Abstand vom C zum H-Atom berechnet sich aus der Differenz des Vektors auf die Position des H-Atoms und des Vektors auf die Position des C-Atoms. Da der Vektor des C-Atoms der Nullvektor ist vereinfacht sich das ganze. Man braucht nur noch den Betrag eines H-Atom-Vektors, zumal alle H-Atome gleichweit vom C-Atom entfernt sind. h1 = [1; 1; 1], c = [0; 0; 0]
dH-C = |h1 - c| = sqrt(1^2 + 1^2 + 1^2) = sqrt(3);
Der Abstand zweier H-Atome voneinander berechnet sich aus der Differenz zweier H-Atomvektoren. Da alle Atome den gleichen Abstand voneinander haben reicht es den Abstand von zwei H-Atomen auszurechnen.
h1 = [1; 1; 1], h2 = [1; -1; -1]
dH-H= |h1 - h2| = | [0; 2; 2] | = sqrt(0^2 +2^2 +2^2) = 2*sqrt(2);
3. Berechnen Sie den Winkel, den das C-Atom und zwei H-Atome miteinander einschließen sowie den Winkel, den jeweils drei H-Atome miteinander einschließen:
Schnittwinkel zweier Geraden:
\( \varphi=\arccos \left(\frac{\overrightarrow{b_{1}} \cdot \overrightarrow{b_{2}}}{|\overrightarrow{b_{1}}||\overrightarrow{b_{2}}|}\right) \)
C-H: Die Geraden verlaufen durch C und H-Atom. Man braucht nur die Richtungsvektoren und die entsprechen den Vektoren auf die H-Atome. Da alle Winkel H-C-H gleich sind reicht es einen davon zu berechnen.
b1 = h1 = [1; 1; 1], b2 = h2 = [1; -1; -1]
b1*b2 = 1*1 +1*(-1) +1*(-1) = -1;
|b1| = sqrt(3); |b2| = sqrt(3);
φ = arccos( -1 / 3 ) = 109,5°; //passt, vgl. https://de.wikipedia.org/wiki/Methan
H-H-H: Nun muss man die Richtungsvektoren zweier Geraden bestimmen, die jeweils durch zwei H-Atome verlaufen und sich in einem davon schneiden. Da auch hier alle H-H-H-Winkel gleich sind, muss man auch nur einen davon berechnen.
h1 = [1; 1; 1], h2 = [1; -1; -1], h3 = [-1; -1; 1]
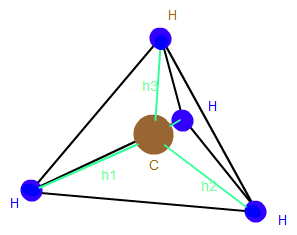
b1 = v1 = h1 - h2 = [0; 2; 2]
b2 = v2 = h1 - h3 = [2; 2; 0]
b1*b2 = 0*2 +2*2 +2*0 =4;
|b1| = 2*sqrt(2); |b2| = 2*sqrt(2);
φ = arccos( 1 / 2 ) = 60°; // passt, da Gleichseitiges Dreieck
Bitte alles kritisch prüfen. Kommentar falls was falsch oder nicht nachvollziehbar ist.