Berechnung von Änderungsgeschwindigkeiten. Höhe y(t) des oberen Endes der Leiter?

Question

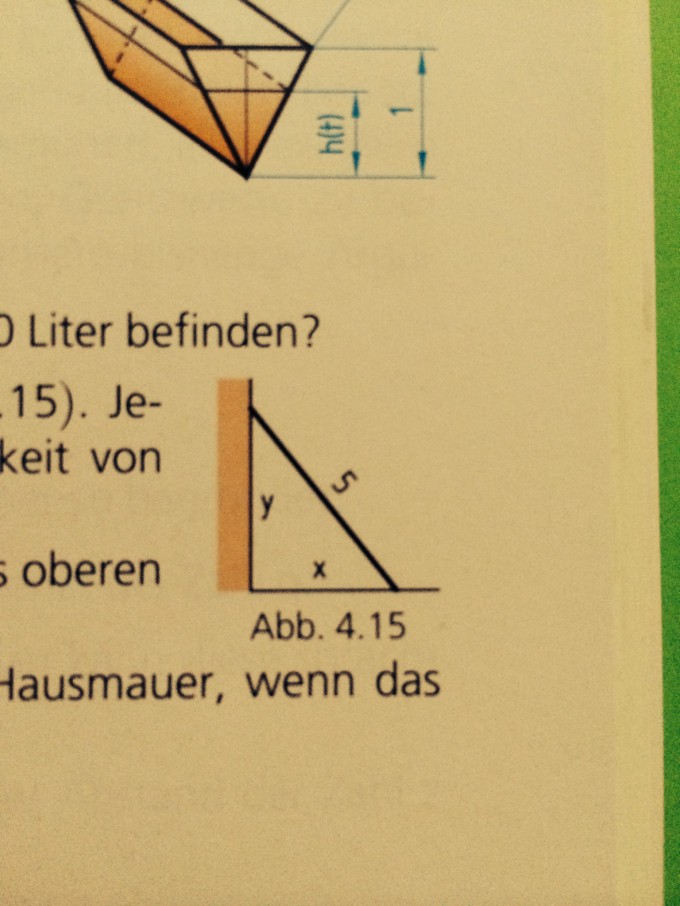
Eine 5 m lange Leiter leht an einer Hausmauer. Jemand zieht das untere Ende der Leiter mit einer Geschwindigkeit von 3 m/s längs des Bodens weg. (Zum Zeitpunkt t=0 sei x=0.)
1) Stelle eine Formel auf, die jedem Zeitpunkt t die Höhe y(t) des oberen Endes der Leiter zuordnet.
2) Wie schnell senkt sich das obere Ende der Leiter längs der Hausmauer, wenn das untere Ende von dieser gerade 3 m entfernt ist.

Ich hätte zur dieser Aufgabe meine Lösung und die Lösung des Heftes. Welche ist die richtige? Wenn die Lösung des Heftes stimmt, dann bitte ich um den Lösungsweg oder den Lösungsweg einer anderen Lösung.

Meine Lösung: y(t) = √(25-(9/4)*t²)
Die des Heftes: y(t) = √(25-9*t²)

Answer 1

x^2 + y^2 = 25      gemäss Pythagoras in Abb. 4.15

y^2 = 25 - x^2

y = √(25-x^2)

x = 3t einsetzen

y(t)  = √(25 - (3t)^2)

Comments

doch wenn x=3 ist und t=0?

---

Das ist nun erst mal y(t). Dort steht: " (Zum Zeitpunkt t=0 sei x=0.) "

Nun musst du erst mal y(t) ableiten und dann überlegen, welches t man bei x=3 einsetzen muss.

Wegen x = 3t , muss gelten 3 = 3t ==> t = 1. 

---

Das kommt vom ungenauen Lesen :D