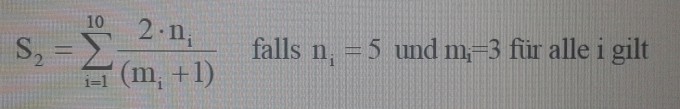Summenberechnung mit 2 Variablen. S= ∑ 2n_(i) : (m_(i) + 1) falls n_(i) = 5 und ,m_(i) = 3 für alle i gilt.

Question

Folgende Aufgabe bereitet mir Kopfzerbrechen:

     10

S= ∑      2n_i : (m_i + 1)        falls n_i = 5 und ,m_i = 3 für alle i gilt.

     i = 1

Erst bin ich davon ausgegangen, dass ich für n_i bzw. m_i  einfach 5 bzw. 3 einsetzen sollte um damit weiter zu rechnen, (sprich: [1x5 : (3x1 + 1)] + [2x5 : (2x3 + 1)] + .......) dann komme ich aber auf unmögliche Ergebnisse (ich glaube, es waren 1071neunzehntel oder so etwas...). Von meinem Dozenten weiß ich, dass am Ende ein ganzzahliges Ergebnis stehen sollte...

Weitere Ansätze habe ich leider nicht, kann mir jemand weiterhelfen?

Answer 1

" falls n_i = 5 und ,m_i = 3 für alle i gilt."

Du musst 10 mal die gleiche Zahl m_(i) und n_(i) einsetzen. 

Daher kannst du gerade so gut einen Summanden ausrechnen und den mal 10 nehmen. 

Zur Kontrolle: Der Summand ist also immer

10/4

und 10*10/4 = 100/4 = 25

Comments

Vielen Dank :)

Ich hatte schon die Vermutung, dass ich es mir schwerer mache, als es sein müsste.

---

Bitte. Gern geschehen. 

Answer 2

Erst bin ich davon ausgegangen, dass ich für n_i bzw. m_i  einfach 5 bzw. 3 einsetzen sollte um damit weiter zu rechnen, (sprich: [2x5 : (3 + 1)] + [2x5 : (3 + 1)] + .......)

also 10 gleiche Summanden, die alle den Wert 2,5 haben, gibt 25