Grenzwertberechnung von (1+(1/x))^x mit x-> ∞

Question

Hi bin mir bei einer Aufgabe ziemlich unsicher

Ich soll den Grenzwert berechnen von lim x-> ∞ (1+ (1/x) )^x

Habe es wie folgt gemacht:  (1+ (1/x) )^ x = e^ (ln(1+(1/x))^ x) = e^ (x*ln(1+ (1/x)) ) mit x-> ∞ folgt

e^ (∞*ln(1)) = e^0 = 1

Ist das so in Ordnung oder habe ich irgendwo einen rechenfehler gemacht?

EDIT(Lu). Habe nach den Caret-Zeichen ^ einen Leerschlag eingefügt, da die Klammern sonst ungeschickt editiert werden. 

Comments

\(\infty\cdot0=0\) ist im Zusammenhang mit Grenzwerten aus gutem Grund keine Rechenregel. Kannst Du ein Gegenbeispiel angeben?

---

stimmt hast recht sonst wäre lim 1/n * lim n^2 = 0 obwohl das gegen unendlich geht.

---

Du kannst wegen der Stetigkeit der e-Funktion den Grenzwert in den Exponenten ziehen und erst mal \(\lim_{x\to\infty}x\ln(1+1/x)\) ausrechnen. Dazu gibt es mehrere Moeglichkeiten. Betrachte z.B. den Ausdruck nach dem Limes als Differenzenquotient von \(\ln x\) and der Stelle \(1\). L'Hospital muesste auch gehen.

---

Mit l´hospital hats geklappt

Answer 1

Das Ergebnis ist dann aber \( e \)

Comments

yup bin auch drauf gekommen

Answer 2

Hallo Situ, 

wenn du dir bei einem Ergebnis unsicher bist, dann lass dir die Funktion doch einfach zeichnen (GTR oder online) bzw. prüfe durch einsetzen von großen x-Werten dein Ergebnis.

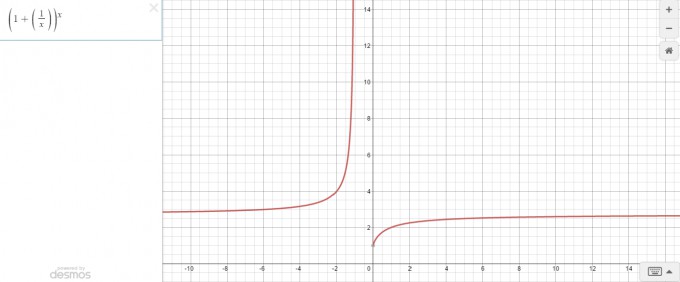
Ich habe deine Funktion mit Desmos online gezeichnet [siehe unten] und man erkennt, dass e der Grenzwert ist. Das ist auf keinen Fall eine Garantie, dass die Rechnung dann auch richtig ist - schließlich kann auch eine falsche Rechnung durch dumme Zufälle bzw. mehrere Fehler zu einem "richtigen" Ergebnis führen. Allerdings hast du  zumindest einen kleinen Anhaltspunkt, falls graphisch etwas anderes herauskommen sollte.

Eingesetzt mit x=100 ergibt sich:
f(100)= [ 1+ ( 1:100 ) ]^100 = ( 1 + 0,01 )^100 = 1,01^100 = 2,7048...
Das Ergebnis kommt wie du siehst ziemlich nahe an e = 2,718...

Hoffe das mein Tipp dir vielleicht weiterhilft ;)

Liebe Grüße