Gegeben sind die Funktionen \( f \) und \( g \) mit
\( f(x)=\sin \left(\frac{\pi}{2} x\right)+1 \text { und } g(x)=-x^{3}+3 \text { mit } x \in \mathbb{R} \)
Ihre Schaubilder heißen \( K_{f} \) und \( K_{g} \).
3.1 Bestimmen Sie die ersten drei Ableitungen von \( f \).
Geben Sie alle Extrem-und Wendestellen von \( K_{f} \) an.
Welche \( y \)-Werte haben die Hoch-, Tief- und Wendepunkte?
3.2 Welche besondere Eigenschaft hat der Wendepunkt von \( K_{g} \) ?
Begründen Sie Ihre Antwort.
Berechnen Sie die Nullstelle von \( g \).
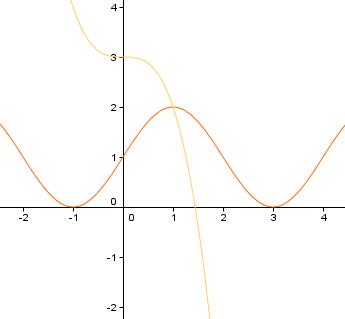
3.3 Ermitteln Sie die Koordinaten des Schnittpunktes von \( K_{f} \) und \( K_{g} \).
Zeichnen Sie \( K_{f} \) und \( K_{g} \) in ein gemeinsames Schaubild.
3.4 \( K_{f}, K_{g} \) und die \( y \)-Achse schließen eine Fläche ein, die von der Geraden \( y=2 \) in zwei Teilflächen geteilt wird.
Ermitteln Sie die Differenz der Flächeninhalte.
3.5 Der Term von \( f \) soll so abgeändert werden, dass der Wertebereich von \( f \) das Intervall \( [0 ; 4] \) bzw. das Intervall \( [-1 ; 5] \) ist. Geben Sie jeweils eine Möglichkeit an.
3.6 Die Funktion \( h \) mit \( h(x)=\sin (a \pi x)+1 \) hat bei \( x=1 \) ihre kleinste positive Nullstelle.
Bestimmen Sie a.
Berechnen Sie für dieses a die zweitkleinste positive Nullstelle von \( h \) exakt.
Ansatz/Problem:
Mein Problem liegt in der Aufgabe 3.3 Aufgabe 3.1-3.2 wurden bereits gelöst.
Ich bin mir nicht sicher ob die Lösung rechnerisch geschehen soll.
Mein Versuch:
\( \sin \left(\frac{p i}{2} * x\right)+1=x^{3}+3 \)
Zum einen weiß ich nicht wie ich das x aus dem sin heraus bekomme und zum anderen bin ich mir wie gesagt nicht sicher ob dies der Richtige Ansatz ist da durch das x^3 die ganze Gleichung so aussieht als sei sie am Ende nicht ohne weitere Schwierigkeiten zu lösen.
Ich hab mir die beiden Funktionen einmal Zeichnen lassen und es ist ersichtlich das der SP bei (1|2) liegt.
Wie komme ich nun in meiner Klausur zur Lösung.... welches Wissen fehlt mir noch?
Könntet ihr mir bitte noch einen Tipp für die Lösungsansätze zu Aufgabe 3.5 und 3.6 geben.