Suche Gleichungen der Tangenten senkrecht zu g. a) k: (x-5)^2 + (y-2)^2 = 100, g: 3x - 4y + 10= 0.

Question

Tangenten des Kreises \( k \) stehen im rechten Winkel zur Geraden \( g \). Bestimme die Koordinatengleichungen der Tangenten.

a) \( k:(x-5)^{2}+(y-2)^{2}=100, \quad g: 3 x-4 y+10=0 \)

b) \( k: x^{2}+y^{2}+16 y-225=0, \quad g:\left(\begin{array}{l}x \\ y\end{array}\right)=\left(\begin{array}{l}3 \\ 7\end{array}\right)+t\left(\begin{array}{c}-8 \\ 15\end{array}\right) \)

Answer 1

Schneide die Parallele zu g durch den Mittelpunkt des Kreises k. mit dem Kreis k. Die beiden so gewonnenen Schnittpunkte sind die jeweiligen Berührpunkte der beiden Tangenten. Das wäre dann der erste Teil.

Answer 2

hier das Ergebnis von Teilaufgabe a.) als Berechnung

  k: (x-5)² + (y-2)² = 100

  g: 3x - 4y + 10= 0.

Zuerst die Umwandlung der Gleichungen in Funktionen

f(x) = y = ± √ ( -x^2 + 10 * x + 75 ) + 2 ( Kreis )

g(x) = y = 3/4 * x + 5/2

f´(x) = ( 5 - x ) / √ ( -x^2 + 10 * x + 75 )

Die Tangente des Kreises und die Gerade g sollen senkrecht aufeinanderstehen, sind also Tangente und Normale.

Für die Steigung gilt :

t = - 1 / n

t =  ( 5 - x ) / √ ( -x^2 + 10 * x + 75 ) = -4/3

x = 13

x = -3

mfg Georg

Answer 3

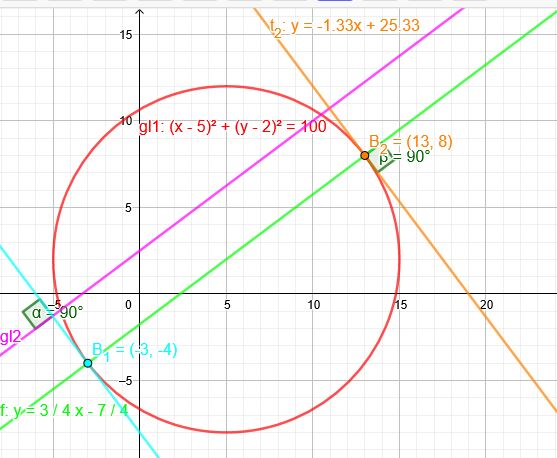
\( k:(x-5)^{2}+(y-2)^{2}=100, \quad g: 3 x-4 y+10=0 \)

\( k(x,y)=(x-5)^{2}+(y-2)^{2}=100\)

\( k_x(x,y)=2(x-5)\)

\( k_y(x,y)=2(y-2)\)

\(k'(x)=-\frac{k_x(x,y)}{ k_y(x,y)}=-\frac{x-5}{ y-2}\)

Die Gerade g hat die Steigung \(m=\frac{3}{4}\)

Tangenten des Kreises \( k \) stehen im rechten Winkel zur Geraden \( g \):   \(m_t=-\frac{4}{3}\)

\(-\frac{4}{3}=-\frac{x-5}{ y-2}\)

\(\frac{4}{3}=\frac{x-5}{ y-2}\)

\(y=\frac{3}{4}x-\frac{7}{4}\)  schneidet den Kreis in den beiden Berührpunkten:

\( (x-5)^{2}+(\frac{3}{4}x-\frac{7}{4}-2)^{2}=100 \)

\(x_1=-3\)    \(y_1=\frac{3}{4}\cdot(-3)-\frac{7}{4}=-4\)

\(x_2=13\)     \(y_2=\frac{3}{4}\cdot13-\frac{7}{4}=8\)

Nun noch die beiden Tangenten berechnen.