Stereometrie: Pyramide in Achtelkugel einbeschrieben. Welches Volumen?

Question

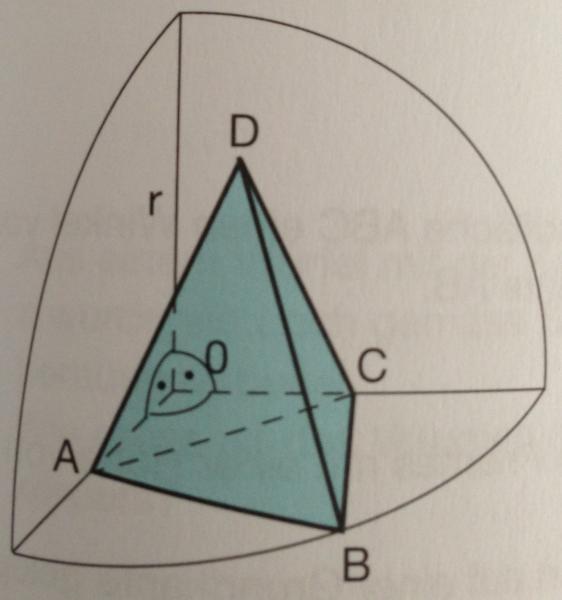
Einer Achtelskugel mit dem Radius r wird eine Pyramide gemäss Skizze einbeschrieben. Die Grundfläche ABC ist ein gleichseitiges Dreieck.

Weiter gilt: AD=BD=CD und OA=OC

D liegt auf der Kugelfläche. Berechnen Sie das Volumen der Pyramide aus r.

Bisheriges Vorgehen: Grundfläche der Pyramide wurde berechnet. Für das Volumen fehlt noch die Höhe der Pyramide, die sich mit dem Radius berechnen lassen kann.

 

Comments

Was genau hast du in der Grundfläche bereits rausbekommen? Alle Eckpunkte?

D hat aus Symmetriegründen von A, B und C denselben Abstand.

Answer 1

Wenn du alle Angaben in der Grundfläche(insbesondere die Eckpunkte der Pyramide schon kennst, sollte das Folgende bereits helfen.

Sei D(x,y,z)

x² + y² + z² = r²

Nun hast du aus Symmetriegründen:

x² + x² + z² = r²

2x² + z² = r²

z² = r² - 2x²

h= z = √(r² - 2x²)