Aufgabe zur Aufstellung einer Gleichung (Analysis). Kanalisation eines Wildbachs.

Question

Aufgabe:

Vor Jahren ist ein Wildbach schnurgerade kanalisiert worden. Der Kanal verläuft entlang einer Geraden k durch die Punkte \( A(0 ; 2) \) und \( B(4 ;-2) \). Der Bach soll in sein altes Bett zurückverlegt werden, das durch die Punkte \( A, C(2 ;-2) \) und \( D\left(\frac{8}{3} ;-2\right) \) verläuft und bei \( B \) wieder in den Kanal mundet.

[Maßstab: 1 LE entspricht 100 m].

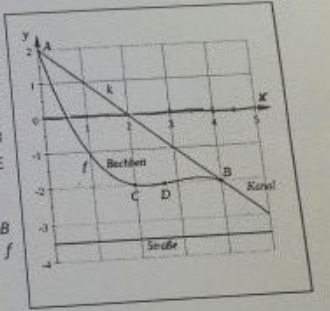
Das Bachbett kann zwischen den Punkten \( A \) und \( B \) durch den Graphen einer ganzrationalen Funktion dritten Grades beschrieben werden.

a) Bestimme eine Gleichung der Funktion \( f \).

Zur Kontrolle; \( f(x)=-\frac{3}{16} x^{3}+\frac{13}{8} x^{2}-\frac{9}{2} x+2 \) mit \( 0 \leq x \leq 4 \)

b) Untersuche, ob der Ubergang zwischen dem Bachbett und dem Kanal im Punkt B
knickfrei ist.

c) Bestimme die Koordinaten des Punktes, in dem das Bachbett sein Krummungsverhalten
ändert.

d) Eine Straße wird im gegeberien Koordinatensystem durch die Gerade mit der Gleichung \( y=-3,5 \) beschrieben. Zwischen Straße und Bachbett soll ein Überschwemmungsgebiet eingerichtet werden. Dafür muss der Abstand zwischen Bachbett und StraBe mindestens
\( 145 \mathrm{~m} \) betragen. Prüfe, ob dies zutrifft.

e) Das Gelande zwischen dem Kanalabschnitt \( A B \) und dem Bachbett soll an einen Fischereiverein für 15 Cent pro Quadratmeter und Jahr verpachtet werden. Bestimme die Höhe der Jahrespacht (ausführliche Darstellung der Berechnung).

Ohne Stammfunktion.

Ich weiß einfach nicht wie ich die Gerade bilden könnte und die anderen Fragen sind mir auch ein Rätsel wie weiße ich nach das es knickfrei ist?

Comments

b.) knickfrei
Kanalgerade : k ( x ) = -x + 2
k ´ ( 4 ) = f ´ ( 4  )

c.)  am Wendepunkt
f ´´ ( x ) = 0

d.)
Tiefpunkt von f bestimmen und prüfen ob der
Funktionswert den geforderten Abstand zur Straße hat.

e.)
ohne Stammfunktion geht es nicht.

∫ k ( x ) - f ( x ) dx zwischen 0 und 4

Answer 1

OK, dann hören wir mal auf, zu philosophieren, und widmen uns der Aufgabe.

a) Die allgemeine Gleichung einer ganzrationalen Funktion dritten Grades ist \(f(x)=ax^3+bx^2+cx+d\), die Koeffizienten \(a,b,c,d\) sind zu bestimmen. Du hast vier Punkte, die auf dem Graphen liegen: Punkte in die Funktionsgleichung einsetzen ergibt ein lineares Gleichungssystem --> lösen.

b) Knickfrei bedeutet: Im Punkt \(B\) haben \(f\) und die Gerade die gleiche Ableitung.

c) Wendepunkt = Punkt, an dem der Graph sein Krümmungsverhalten ändert

d) Was du da machen musst, findest du raus, wenn du dir die Skizze genau anschaust.

e) Flächeninhalt durch Integration berechnen. Was ist mit "ohne Stammfunktion" gemeint?

Viel Spaß beim Rechnen!

Comments

Ohne Stammfunktion ? Wahrscheinlich müssen wir die Stammfkt nicht herleiten sondern einfach nur in den Taschenrechner eingeben den wie soll ich den Flächeninhalt ohne Stammfkt berechnen?

---

Ich hoffe, dass das nicht so gemeint ist.
Das würde ja sehr viel Sinn machen im Matheunterricht: "Das müsst ihr nicht selber rechnen. Ihr müsst nicht wissen, was da passiert oder wie das funktioniert, der Taschenrechner kann das ja. Und ihr müsst das auch nicht per Hand rechnen können." (Ironie off). Wobei, wundern würde mich sowas wahrscheinlich nicht mehr...

Answer 2

zu a) ist ja wohl genug gesagt.

b) f ' (x) = -9/16 x^2 +13/4 x -9/2 also f ' (4) = -1/2 aber die

gerade hat die Steigung -1 . Also nicht knickfrei.

c) f ' ' (x) = 13/4 - 9/8 x  = 0  gibt x = 26 / 9 Also ist der Punkt ( 26/9  ;  -476/243 )

d) f ' (x) = 0 gibt ungefähr 2,3 oder 3,5 .

Der Tiefpu. ist bei (2,4  ; -2,035) also hier mehr 146m Abstand.

Aber wie ist es am Rand bei x=4 ? Dort sind es 150m, also auch genug.

e) Für die Fläche :

Integral von 0 bis 4 über  ( -x + 2) - f(x)  dx gibt 41/12 also etwa 3,4167 ha.

Denn die Längeneinheit ist 100m, also Fläche in ha.

Das sind 34167 m^2 also 5125,05 Euro als Miete.