Bestimmen der Gleichung einer linearen Funktion die in x= -1,5 knickfrei in f(x)=-2x² + 1,3x übergeht

Question

Bestimmen sie die Gleichung einer linearen Funktion die in x=-1,5 knickfrei in f(x)=-2x² + 1,3x übergeht.

Hilfe!

Answer 1

Hi,

knickfrei bedeutet, dass wir die gleiche Steigung haben.

Es muss also f'(1,5) der Steigung m der Geraden g: y = mx+b entsprechen.


f'(x) = -4x+1,3

f'(1,5) = -4,7 = m


Zudem wissen wir, dass die Gerade ja bei P(1,5|f(1,5)) ansetzen soll. -> P(1,5|-2,55)

-2,55 = -4,7*1,5 + b

b = 4,5


Die gesuchte Gerade lautet also y = -4,7*x+4,5

Zum Anschauen:

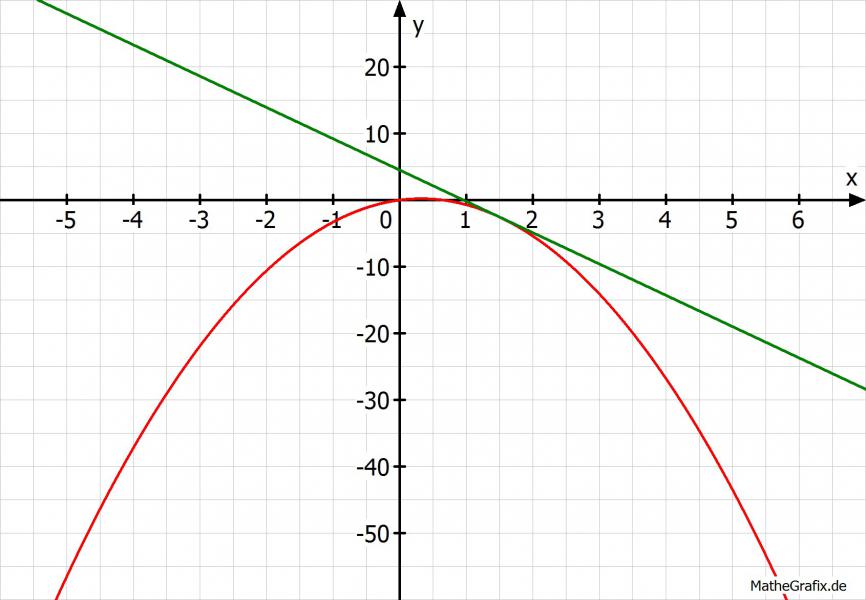
Grüße