Besucher eines Schnellrestaurants: f(x) = - 0.04·x^3 + 0.5·x^2 + 15·x - 160

Question

Die Zahl der Besucher eines Schnellrestaurants, das um 10 Uhr öffnet und um 21:30 Uhr schließt wird mit Hilfe der unten stehenden Grafik beschrieben.

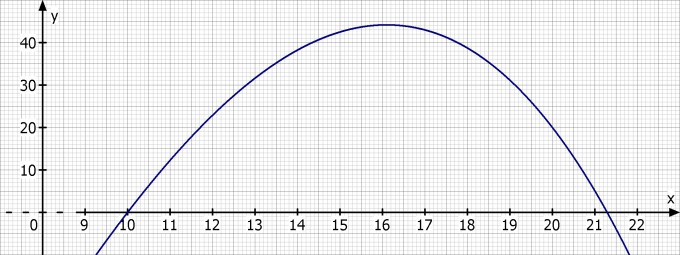
Die zugehörige Funktionsgleichung lautet:

f(x) = - 0.04·x^3 + 0.5·x^2 + 15·x - 160

a) Bestimme die Zahl der Besucher zwei Stunden nach Öffnung des Schnellrestaurants.

f(12) = 22.88 also ca. 23 Personen

b) Wann betritt die erste Person das Schnellrestaurant, wann verlässt die letzte Person das Schnellrestaurant.

f(x) = - 0.04·x^3 + 0.5·x^2 + 15·x - 160 = 0

x = 10 also 10 Uhr

x = 21.29 also etwa 21:17 Uhr

c) Wann ist die Zahl der Besucher am größten? Wie viele Gäste halten sich dann im Restaurant auf?

f'(x) = - 0.12·x^2 + x + 15 = 0

x = 16.10 also ca. 16:06 Uhr

f(16.10) = 44.17 also ca. 44 Personen

Comments

Was ist genau die Frage? :-)

---

Duplikat exakt gleich?

Titel: Anwendungsaufgabe Funktion

Stichworte: anwendung

Aufgabe:

Die Zahl der Besucher einer Pizzeria, die um 10 Uhr öffnet und um 21:30 Uhr schließt, wird durch folgende Funktion beschrieben :

f(x) = -0,04 x^3 + 0,5 x^2 + 15 x - 160

x [10;21,5]

f(x) Anzahl der Besucher

a. Bestimmen sie die Zahl der Besucher zwei Stunden nach der Öffnung der Pizzeria

b. Bestimmen sie die durchschnittliche Änderung der Besucherzahlen in den ersten drei Stunden

c. Geben sie an, wann die Zahl der Besucher am größten ist und wie viele Gäste zu dieser Zeit in der Pizzeria sind

Wie geht das?

---

Duplikat oder Scheinduplikat?

---

Wie kommst du auf 16.10 ?? Bzw. 16:06 ?

---

1/10 von einer Stunde sind 6 Minuten.

D.h. 16.10 Stunden = 16 Stunden und 6 Minuten.

Answer 1

Hallo,

b) erster Besucher kommt bzw. letzter Besucher geht:: 

Hier ist vielleicht  f(x) = 0,5  sinnvoller.

x ≈ 10,039  also  zwischen 10:02 und 10:03 Uhr

x ≈ 21,261 also zwischen 21:15 und 21.16

Wenn man aber davon ausgeht, dass die Funktion so erstellt wird,  dass bei jeder Änderung der Besucherzahl ein Punkt im Graph eingetragen wird, wäre wohl im ersten Fall f(x) =1, im zweiten Fall f(x) = 0 der sinnvollste Ansatz.

Wie auch immer, es ist halt eine interpolierte Funktion und damit sind alle Diskussionen spekulativ.

Gruß Wolfgang

Answer 2

a) f(12)=22,88 , also etwa 23 Besucher um 12h.

b)  (f(13)-f(10)) / ( 13 - 10 ) =31,6  / 3 = 10,5

c)  f ' (x) = 0  <=>    x = 16,1    und f ' ' (16,1) < 0 also Maximum bei 16.1

Um 16:06 Uhr ist die Besucherzahl maximal,

es sind f(16.1)=44 Stück.

Comments

Und der Rechenweg bei b) ??

---

Ableitung bilden, gleich 0 setzen und

mit abc-Formel ausrechnen.

---

Abc - Formel?

---

Formel zum Lösen einer quadratischen Gleichung.

Mitternachtsformel ?

---

Und wie macht man das damit?