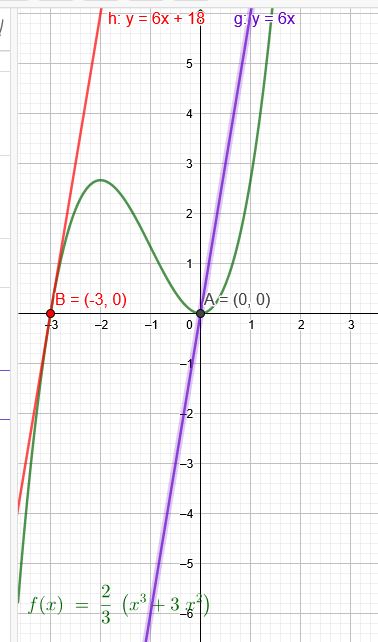
Bestimme die Gleichung einer ganzrationalen Funktion 3.Grades deren Graph die x-Achse im Ursprung berührt und deren Tangente in \(P(-3|0)\) parallel zu \(y=6x\) ist
\(f(x)=a*[x^2*(x+3)]=a*[x^3+3x^2]\)
\(f´(x)=a*[3*x^2+6x]\)
\(f´(-3)=a*[3*(-3)^2+6*(-3)]=a*[9]=6\) \(a=\frac{2}{3}\)
\(f(x)=\frac{2}{3}*(x^3+3x^2)\)