Gebrochen rationale Funktionen Limes berechnen

Question

Folgende Funktion:

f(x)=(2x+2)/(x^2-1)

Was ist die maximal mögliche Definitionsmenge?

Wie ist das verhalten des Graphen in der Nähe der Definitionslücken?

Und wie kommt man da jeweils drauf?

!

Comments

Tipp: x² - 1 = (x - 1)·(x + 1).

---

das bedeutet doch, dass die definitionslücken bei 1 und -1 liegen, aber wenn ich den Graphen mit einem Funktionsplotter plotte, ist da keine definitionslücke bei -1...

---

Das liegt daran, dass der Funktionsplotter die Funktion bei x=-1 automatisch stetig ergänzt. Das funktioniert, da du bei x=-1 eine hebbare Definitionslücke hast, was du daran erkennen kannst, dass in der Funktion x=-1 Nullstelle von Zähler und Nenner ist.

---

Kürze  x + 1.

---

@Yakyu: Es stimmt also aber trotzdem, dass bei x=-1 eine definitionslücke ist und dass sich der graph im Bereich dieser definitionslücke von beiden seiten -1 annähert?

---

Ja.                      

---

Genau genommen stimmt das.  Aber die Aufgabe möchte trotzdem darauf hinaus,  dass die maximale definitionsmenge R\{1} ist. 

---

ok, vielen herzlichen Dank!

Answer 1

f(x) = (2·x + 2)/(x^2 - 1)

f(x) = 2·(x + 1)/((x + 1)·(x - 1))

Behebbare Definitionslücke

f₂(x) = 2/(x - 1)

Maximale Definitionsmenge D = R \ {1 ; -1}

Wie ist das verhalten des Graphen in der Nähe der Definitionslücken?

lim (x --> -1) f(x) = f₂(-1) = 2/-2 = -1

lim (x --> 1-) f(x) = 2/(0-) = -∞

lim (x --> 1+) f(x) = 2/(0+) = ∞

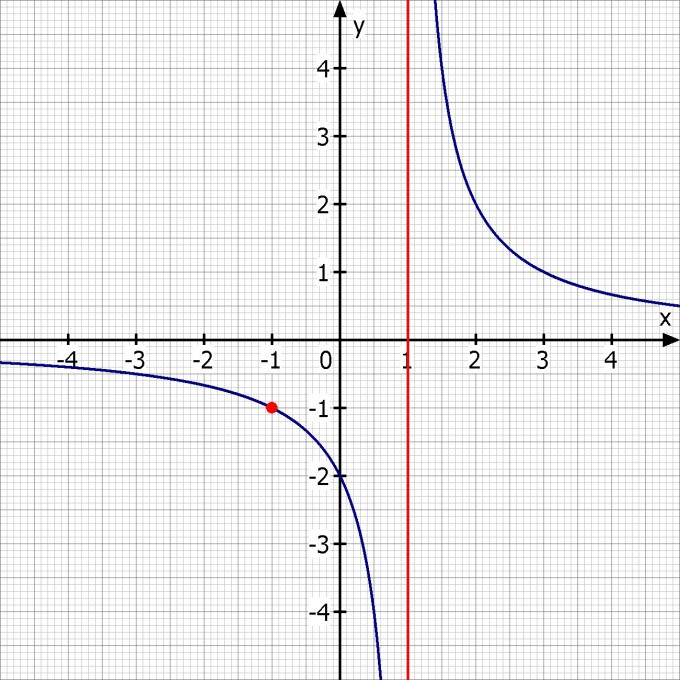
Skizze