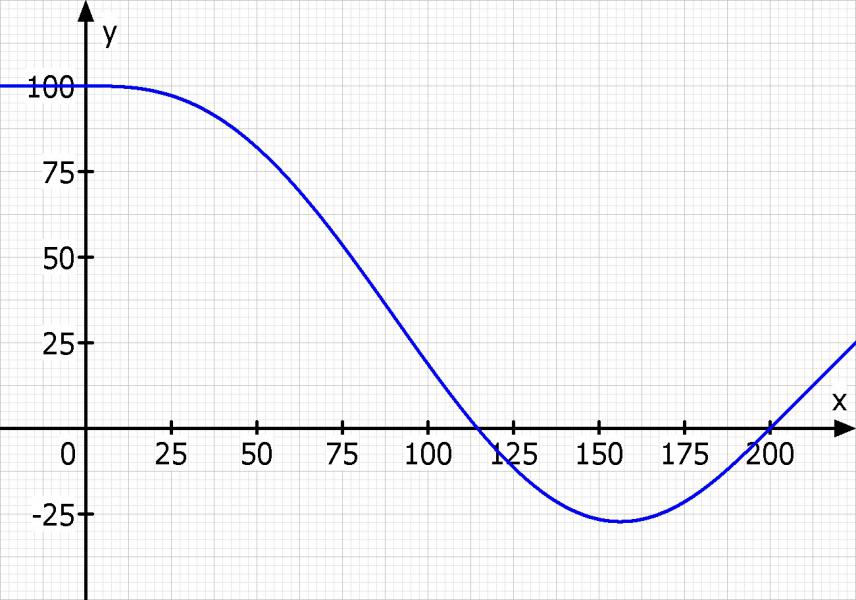
Am Ende von Straße 1
f(0) = 100
f'(0) = 0
f''(0) = 0
Am Anfang von Straße 2
f(200) = 0
f'(200) = 1
f''(200) = 0
Ich brauche bei 6 Bedingungen eine Gleichung 5. Grades
f(x) = ax^5 + bx^4 + cx^3 + dx^2 + ex + g
f'(x) = 5·a·x^4 + 4·b·x^3 + 3·c·x^2 + 2·d·x + e
f''(x) = 20·a·x^3 + 12·b·x^2 + 6·c·x + 2·d
Ich setzte die obigen Bedingungen um in ein Gleichungssystem
g = 100
e = 0
2·d = 0
320000000000·a + 1600000000·b + 8000000·c + 100 = 0
8000000000·a + 32000000·b + 120000·c = 1
160000000·a + 480000·b + 1200·c = 0
Wir lösen das LGS und erhalten die Lösung
a = -3/800000000 ∧ b = 29/16000000 ∧ c = -9/40000 ∧ d = 0 ∧ e = 0 ∧ g = 100
a = -3.75·10^-9 ∧ b = 1.8125·10^{-6} ∧ c = -2.25·10^-4 ∧ d = 0 ∧ e = 0 ∧ g = 100
f(x) = -3/800000000·x^5 + 29/16000000·x^4 - 9/40000·x^3 + 100
Skizze: