Wasserbeckenaufgabe überprüfen und Ansatz

Question

bei a habe ich für den Funktionsterm:

v(t)= 70e^{-0,007t}

Und die Wassermenge nimmt ab, da v'(t) ein negatives Vorzeichen hat und da die Ableitung die Steigung angibt, nimmt die Wassermenge ab.

Es ist außerdem mit einem Volumen von 30m^3 zu rechnen.

Bei b habe ich keine Ahnung.

Vielleicht: v'(t)=0,07(-10000-v(t))

Danke schonmal 

Answer 1

b) 

v(t)= - 0,49*e^-0,007t    

Stammfunktion wäre

V(t) = -0,49/ -0,007 *e^-0,007t    + c

=70 *e^-0,007t    + c 

Du hast die Konstante vergessen.

also bei t=0 hast du 100
deshalb  v(t)     =70 *e^-0,007t    + 30

v ' (t) = 70*(-0,007)*e^-0,007t     = -0,49*e^-0,007t    

v ' (t) =0,007(a-v(t) )

= 0,007 (a - v(t) - 30 )

also richtig für a=30.

also konstanter Zufluss von 30 m^3 pro Stunde .

d) langfristig 50 heißt

für x gegen unendlich geht v(t) gegen 50.

70 *e^-0,007t    + c für x gegen unendlich wäre c

also c=50.

Comments

hallo mathef,

V ( t )  = 70 *e^-0,007t    + 30

c.) die Schlußfolgerung das ein konstanter Zufluß vorhanden ist
erschließt sich mir noch nicht.

Es geht doch :

Zufluß bei t −> ∞ [ 70 *e^-0,007t  ] = 0
Abfluß keiner.

Die Aussage in c. soll wohl aus b. geschlossen werden ???

---

Richtig, da hatte ich mich etwas vertan.

Aus  v ' (t) =0,007(a-v(t) )

v ' (t) =0,007a- 0,0007*v(t)

folgt es. Denn 0,0007*a ist ja konstant,

und wegen a=30 ist also der konstante Zufluss 0,021 m^3 / h .

---

Ich habe den Sachverhalt noch nicht verstanden.

Gegeben
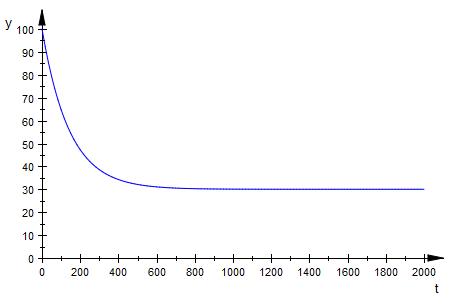
V ( t )  = 70 *e^-0,007t    + 30
V ´( t ) = v ( t ) = - 0,49*e^-0,007t    

Ich kann V ´ ( t ) = v ( t ) auch umformen zu
v ( t ) = 0,007 * ( a - V ( t ) )
v ( t ) = 0,007 * ( a -  ( 70 *e^-0,007t    + 30 ) )
Nur falls a = 30 ist gilt
v ( t ) = 0,007 * ( 30 -  70 *e^-0,007t   - 30  )
v ( t ) = 0,007 * ( - 70 *e^-0,007t  )
V ´( t ) = v ( t ) = - 0,49*e^-0,007t    

Dieser Nachweis wurde in b.) verlangt.

c.) wie kann man daraus oder überhaupt  schließen " das die Veränderung
auf einem konstanten Zufluß und einem zeitabhängigen Abfluß basiert " ?

---

Denkbar wäre doch :
Zufluß bei t = 0 gleich 0. Es fließt gar nichts mehr zu.
Gemäß dem hydrostatischen Druck im Behälter fließt
zunächst viel ab und dann weniger.

---

Die Diff.gl war doch

v ' (t) =0,007(a-v(t) )

bzw.          v ' (t) =0,0007a- 0,0007*v(t)

Und das ist die Änderungsrate des Volumens.

Diese ist eine Differenz aus einer positiven Konstanten 0,0007a

(Das ist dann wohl der konstante Zufluss)

und davon subtrahiert wird  0,0007*v(t)

das ist dann der variable Abfluss.  ???? oder???