Wie zeichne ich : 2x-y=0 und x-2y=0?

Question

Wie kann ich das lösen da dieSsteigung nur x ist-wie zeichne ich das?

Answer 1

Hi,

Deine erste Aufgabe bei sowas sollte sein, nach y aufzulösen. Dann hast Du die Geradenform y=mx+b vorliegen.

 

2x-y=0 |+y

y=2x

 

x-2y=0 |+2y

2y=x     |:2

y=x/2

 

 

Nun siehst Du direkt, dass beide Geraden durch den Ursprung gehen, da kein y-Achsenabschnitt b vorhanden ist.
Die Steigung m kann man als Vorfaktor von x identifizieren und bedeutet so viel wie: "Gehe eins nach rechts und um so viel nach oben (oder bei negativen Vorzeichen nach unten) wie der Vorfaktor groß ist".

 

In ersterem Falle wäre das also 1 nach rechts und 2 nach oben.

Im zweiteren Falle wäre das also 1 nach rechts und 1/2 nach oben.

 

Sollte letztlich so ausschauen:

 

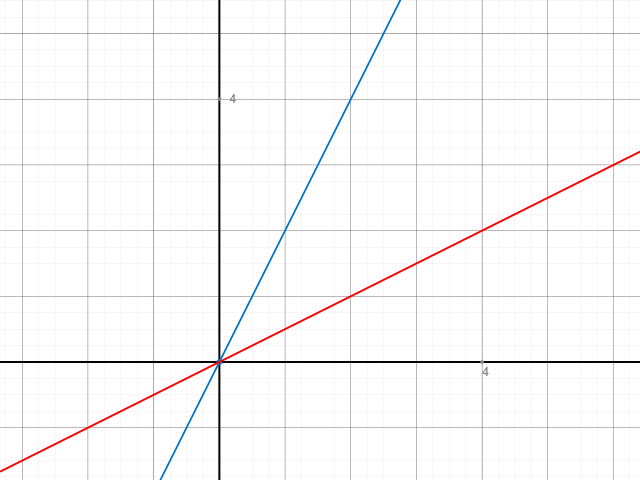
Du könntest das übrigens auch über eine Wertetabelle bestimmen. Bestimme Dir einfach zwei Punkte und markiere sie im Schaubild. Schon kannst Du Deine Gerade durchlegen (als ersten Punkt würde ich hier den Ursprung wählen. Den brauchst Du ja nicht zu berechnen. Als zweiten Punkt nehme z.B. x=2 und errechne den y-Wert. Dann damit ins Schaubild.).

 

P.S.: Roter Graph entspricht y=x/2 und folglich der blaue Graph y=2x.

 

 

Grüße

Comments

Prima Antwort. Hier vielleicht noch eine etwas bessere Skizze:

---

Also kann man die gerade nicht direkt an der gleichung ablesen?

 

und wie kann man ablesen wie viele lösungen ein lgs hat?

z.b.: 2x+3y=9  und  12x+15y=3
        x-y=2                 4x+5y=1

dank der lösungen weis ich was rauskommt kann mir dies nur nicht erklären..

---

2x+3y=9
x-y=2

Hier gibt es eine Lösung weil die werte vor x und y nicht linear abhängig sind.

12x+15y=3
4x+5y=1

Hier gibt es unendlich viele Lösungen, weil ich die untere Gleichung mit 3 multiplizieren kann und dabei genau die obige Gleichung herauskommt.

Jetzt mal

12x+15y=3
4x+5y=2

Hier gibt es jetzt keine Lösung. Die Werte vor x und y sind linear abhängig, weil die linke Seite der Unteren Gleichung mal 3 genau die linke Seite der oberen Gleichung ergibt. Allerdings gibt der rechte Teil vom 3 nicht den oberen rechten Teil. Daher gibt es hier keine Lösung.

---

was heißt nicht linear abhängig?

 

und zu meiner ersten frage :Also kann man die gerade nicht direkt an der gleichung ablesen?

---

Zu Deiner ersten Frage;

Nun, mit Übung kann man das natürlich direkt ablesen. Generell würde ich aber die Frage mit "Nein" beantworten und würde Dich aufforden, die von mir getätigten Umformungen vorzunehmen ;).
Erst damit kann man es ganz sicher "direkt ablesen".

 

Wenn Dir der Begriff "linear abhängig" nicht bekannt ist, ist das etwas schwieriger (der Begriff wird mit Sicherheit bald im Unterricht auftauchen).

Bedenke hier zum Beispiel:

12x+15y=3
4x+5y=2

Dass die untere Gleichung (linke Seite) das gleiche aussagt, wie die obere. Es wurde nur durch 3 geteilt. Eine Gleichung ändert sich ja nicht, wenn man durch 3 teilt! 
Nichtsdestotrotz gibt es Probleme mit der rechten Seite. Multipliziert man die untere Gleichung mit 3, haben wir 12x+15y=6. Das heißt die beiden Aussagen der beiden Gleichungen sind nicht gleich und damit gibt es keine Lösung für dieses Gleichungssystem (Diese Argumentation kann nur benutzt werden, wenn die linke Seite (mit x und y) identisch sind).

---

Gerne :)     .

---

sry das ich so viel frage aber ich schreibe morgen die arbeit und das ist das einzige das ich nicht verstehe..

 

also entspricht 2x=2/1 (zwei eintel) also eins nach rechts und 2 nach oben

und bei den aufgaben 2x+4y=-8 und 2.5x-0,5y=3  gibt es ja noch weitere zahle (-8/3)

wie macht man das da? also das man die zugehörige gerade zeichnen kann?

---

Ich zeigs Dir mal für die erste Gerade. Du probierst es dann für die zweite. Einverstanden? ;)

 

Löse nach y auf:

2x+4y=-8     |-2x

4y=-8-2x      |:4

y=-0,5x-2

 

Nun gibt es wieder mehrere Möglichkeiten.

1. Nimm Dir zwei beliebige x-Werte und bestimme den zugehörigen y-Wert. Damit ab ins Schaubild und die beiden Punkte eintragen. Nun noch verbinden und fertig ist die Gerade.

 

2. Der y-Achsenabschnitt (also der Schnittpunkt mit der y-Achse) ist zu finden bei S_y(0|-2). Begib Dich dorthin. Nun trage die Steigung m=-0,5 ab. Wie erwähnt -> 1 nach rechts und 0,5 nach unten (Nach unten wegen dem negativen Vorzeichen).

 

Klar?

 

---

2,5x-0,5y=3   |-2,5x

-0.5y=3-2,5x  |:(-0,5)

       y=6-5x

---

Vorsicht! Du dividierst durch -0,5. Die Vorzeichen der rechten Seite müssen demnach gedreht werden.

Sonst aber richtig. Also y=5x-6

 

Du kannst es dann mit einer der beiden oben genannten Varianten zeichnen? ;)

---

Noch als Schaubild zum Kontrollieren:

---

Ok vielen Dank..

Ich habs verstanden :D

---

Freut mich :).

Viel Erfolg bei der Arbeit.