Ableitungsaufgabe mit Funktionen. Photosynthese: Abgegebene Sauerstoffmenge hängt von der Tageszeit ab.

Question

Bäume geben aufgrund der Fotosynthese Sauerstoff an ihre Umgebung ab. Die abgegebene Sauerstoffmenge hängt von der Tageszeit bzw. vom Licht ab. Die Funktion V mit V(t) = -1,2t^3 + 24t^2 + 10t (V(t) in l; t in h) gibt näherungsweise die Gesamtsauerstoffmenge in Litern an, die ein Baum im Laufe eines Tages nach dem Sonnenaufgang (t=0) abgibt.

a) Bestimme V'(4). Welche Bedeutung hat V'(4) im Sachzusammenhang? 

b) Bestimme den Zeitpunkt t0, für den die Ableitung der Funktion V null ist. Interpretiere den Punkt P(t0|V(t0)) im Sachzusammenhang. Schränke den Definitionsbereich der Funktion V sinnvoll ein.

c) Bestimme näherungsweise den Zeitpunkt, an dem die Sauerstoffproduktionsgeschwindigkeit des Baumes am größten ist. Wie lässt sich das Ergebnis im Sachzusammenhang begründen? Wie groß ist die Sauerstoffmenge insgesamt an diesem Tag an diesem Zeitpunkt?

Answer 1

Die Funktion V mit V(t) = -1,2t³ + 24t² + 10t (V(t) in l; t in h) gibt näherungsweise
die Gesamtsauerstoffmenge in Litern an, die ein Baum im Laufe eines Tages
nach dem Sonnenaufgang (t=0) abgibt.

a) Bestimme V'(4). Welche Bedeutung hat V'(4) im Sachzusammenhang? 

V ´( t ) = -3.6 * t^2 + 48 * t + 10
V ´( 4 ) = -3.6 * 4^2 + 48 * 4 + 10
V ´( 4 ) = 144.4 l / h

Sauerstoffproduktion um 4 h in l / h

b) Bestimme den Zeitpunkt t0, für den die Ableitung der Funktion V
null ist. Interpretiere den Punkt P(t0|V(t0)) im Sachzusammenhang.
Schränke den Definitionsbereich der Funktion V sinnvoll ein.

V ´ ( t ) = 0
-3.6 * t^2 + 48 * t + 10 = 0
t = -0.21 h
und
t = 13.54 h

( -0.21 | -1.03 )
(  13.54 | 1556 )

Der erste Wert würde eine Sauerstoffaufnahme bedeuten:
Ob dies möglich ist weiß ich nicht.

Falls ich mich nicht irgendwo verrechnet habe.
Ich hege Zweifel an der Ausgangsformel.
Es müßte eine Formel für eine periodische 24 h Funktion sein
Dies aber nicht der Fall.

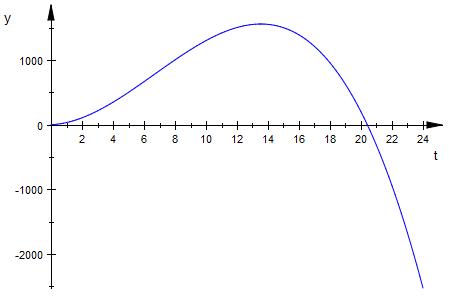
Vielleicht ist es sinnvoll den Def-Bereich bei 20.5 enden zu lassen.

c) Bestimme näherungsweise den Zeitpunkt, an dem die
Sauerstoffproduktionsgeschwindigkeit des Baumes am größten ist.
Wie lässt sich das Ergebnis im Sachzusammenhang begründen?
Wie groß ist die Sauerstoffmenge insgesamt an diesem Tag an
diesem Zeitpunkt?

Sauerstoffproduktionsgeschwindigkeit = Steigung am steilsten = Wendepunkt
V ´´ ( t ) = 48 - 7.2 * t
48 * 7.2 * t = 0
t = 6  2/3 h

6  2/3 h nach Sonnenaufgang ist  Sauerstoffproduktion am größten:
Diese kannst du berechnen mit V ´( 6  2/3 ) = ?

Und zuletzt
∫ V ( x ) dx zwischen 0 und 20.5

Bin bei Bedarf gern weiter behilflich.