Bestimmung der Wendepunkte einer gebrochen rationalen Funktion. f(x) = (4-x^2) / (2+x^2 )

Question

Aufgabe

Gegen ist die Funktion f durch \( f(x)=\frac{4-x^{2}}{2+x^{2}} \) .

Der Definitionsbereich der Funktions f ist Teilmenge der reellen Zahlen.

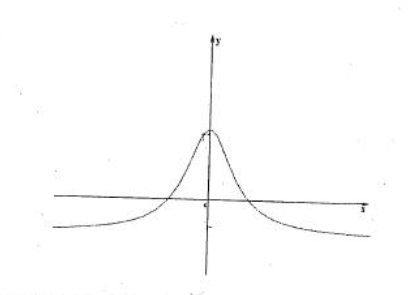
2.1 Bestimmen Sie den Definitionsbereich der Funktion f und das Verhalten im Uendlichen. Geben Sie das Symmetrieverhalten des Graphen an!

2.2 Berechnen Sie die Koordinaten der Schnittpunkte mit den Achsen!

2.3 Geben Sie die Gleichung der Asymptote an!

2.4 Berechnen Sie die Wendepunkte. Auf den Nachweis wird verzichtet.

ich bin bei der unten stehenden Aufgabe mittlerweile bei 2.4 Angekommen.

Um die Wendepunkte zu bestimmen habe bis zur 2. Ableitung abgeleitet was sich als ziemlich viel Schreibarbeit durch Ausmultiplizieren herausgestellt hat.

Da es sich um Aufgaben zur Prüfungsvorbereitung handelt bin ich mir ziemlich sicher das mein Ansatz zu kompliziert ist zumal ich nicht nicht weiß wie ich von der 2. Ableitung jetzt die 0 Stellen bestimmen soll.

Unterhalb der Aufgabenstellung hab ich mal meinen Versuch eingefügt ich hoffe es ist lesbar genug :-).

Wie muss ich weiter vorgehen?

Answer 1

Naja, ich denk Du hast da alles richtig gemacht.

Aber um das schneller hinzukriegen machst Du am besten folgendes:

Den Nenner multiplizierst Du am besten nicht aus. Nach der Quotientenregel musst Du ihn bei jeder Ableitung einfach nur quadrieren. Das lässt Du einfach mal so stehen.

Dann bildest Du die zweite Ableitung. Zähler nicht ausmultiplizieren. Dann kannst Du (2+x^2) ausklammern und kannst dann mit dem Nenner kürzen. Im Zähler steht dann nur noch eine quadratische Gleichung und da kannst Du leicht die Nullstellen bestimmen:

2. Ableitung Zähler: (36*x^2 - 24)

2. Ableitung Nenner: (x^2 + 2)^3

 

lg JR