Ich möchte die Punkte A und B eines Dreiecks in einem Koordinatensystems berechnen und gegeben sind folgende Werte als variablen:
Punkt C, die Höhe, den Höhenschnittpunkt, alle Winkel.
Ich habe zunächst angefangen die lineare Funktion hc bestimmt und davon die Orthogonale bestimmt, um eine Funktion für meine Seite c zu haben. Danach habe ich mit Die steigungen der Seiten a und b mithilfe eines Tagens des Winkels zur X-Achse gebildet. Nun habe ich mithilfe von meinem Punkt c und der jeweiligen Steigung den y-Achsenabschnitt der jeweiligen Formeln gebildet und mithilfe von gleichsetzen und einsetzen der Formel X und Y meiner Punkte bestimmt.
Die Winkel meines Dreiecks stimmen immer, nur scheinen die X-Koordinaten komplett daneben zu liegen, je höher/niedriger irgendwelche Steigungen sind und ich komme einfach nicht auf den Rechenfehler.
Anders gesagt: Die Punkte A und B sollen auf meiner Orthogonale liegen, was sie nicht tun (bzw. nur bei 2 bestimmten Winkeln). Sie liegen immer auf einer parallelen geraden zur Orthogonalen.
Falsch:
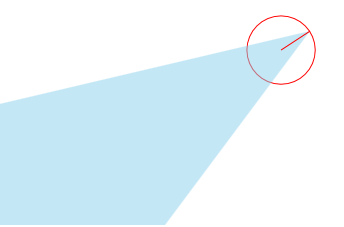
(etwa) Richtig:
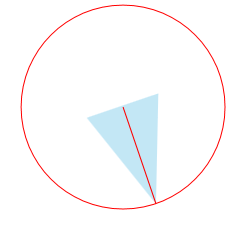
1. Frage: ist der Gedankengang richtig?
2. Frage: sind meine Formeln korrekt?
Steigung Berechnen durch 2 Punkte: m= (y2 - y1) / (x2 - x1)
Steigung mithilfe eines Winkels berechnen: tan(alpha)
Y-Achsenabschnitt berechnen: b= -(m * x - y)
X Berechnen: x= (b1 - b2) / (m1 + m2)
Y Berechnen: y = m*x+b
Ich habe das ganze in einer Programmiersprache realisiert. Vielleicht kann mir ja irgendjemand Denkanstößte geben, wo ich einen Fehler eingebaut habe.