Trigonometrie: Spieleprogrammierung. Objekte mit verschiedenen Winkeln und Geschwindigkeiten

Question

Folgendes Problem:

2 Objekte liegen in einem Koordinatensystem mit jeweils bekannten Koordinaten (AX, AY, BX, BY)

Distanz zwischen Objekten ist ebenfalls bekannt und beträgt X Pixel.

Objekt A bewegt sich mit bekannter Geschwindigkeit AS, gemessen in Pixel pro Frame und kann sich in 45° Schritten in jede Richtung bewegen. Winkel von 0° entspricht der Zeichnung, Winkel von 90° wäre nach oben zeigend.

Objekt B kann sich in jede Richtung frei bewegen und fliegt mit der bekannten Geschwindigkeit BS, ebenfalls in PIxel pro Frame.

Gesucht ist der Winkel von B, der dafür sorgen würde, dass sich die beiden Objekte treffen, wenn sie ihre Richtung nicht mehr ändern und so weiterfliegen wie bisher. Objekt B ist hierbei in jedem Fall immer schnell als Objekt A.

Habe leider keine Vorstellung wie ich an das Problem herangehen soll. Hab scheinbar in Trigonometrie nicht genug aufgepasst. Ich brauche das ganze, wie schon in der Überschrift erkennbar für eines meiner Spiele, die ich derzeit programmiere. Ich hoffe, dass mir hier jemand beim Ansatz helfen kann.

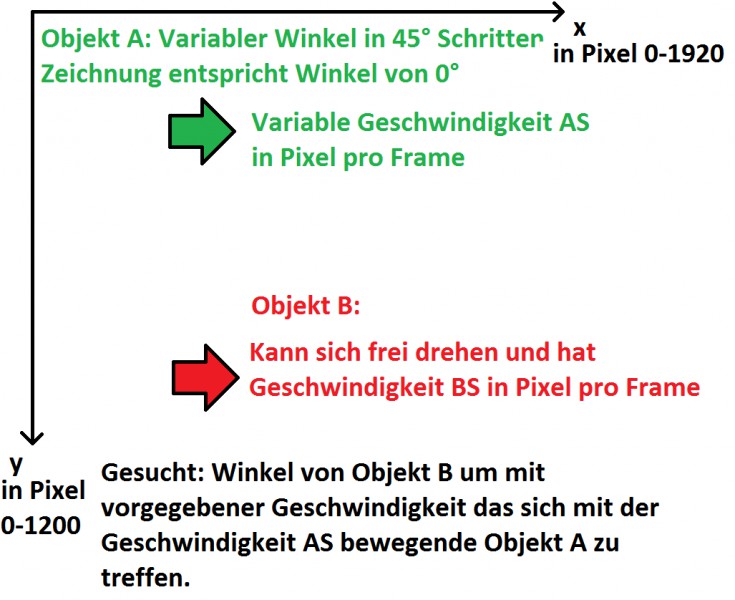
Hier noch eine, hoffentlich einleuchtende Skizze:

Comments

Falls du mehr über die Anwendung von Vektoren in Spielen lernen möchtest, um diese dann selbst zu programmieren, kann ich dir diese Seite wärmstens empfehlen: http://www.tonypa.pri.ee/vectors/start.html (die Programme sind in Actionscript verfasst).

Ansonsten schau dir auch ein paar der Vektorenprogramme an: https://www.matheretter.de/mathe-programme#vek.html

Schöne Grüße
Kai

Answer 1

Der Flugvektor von A ist

[cos(α), sin(α)]

Richtungsvektor

AB = [Bx - Ax, By - Ay]

Winkel zwischen Flugvektor A und Objekt B

γ = arccos (([Bx - Ax, By - Ay] * [cos(α), sin(α)]) / |[Bx - Ax, By - Ay]|)

Nun gilt nach dem Sinussatz (B fliegt in Richtung )

sin(β) = BS / AS * sin(γ)

Nun muss man β noch auf Bildrichtung Normieren.

Ich müßte also in folgende Richtung fliegen: 180 + γ + β

Schau mal ob du das nachvollziehen kannst.
Ich hoffe ich habe da keine groben Rechenfehler drin. Am besten ist das dann immer an Beispielen zu verifizieren.

Comments

Danke für die super antwort.


γ = arccos = (([Bx - Ax, By - Ay] * [cos(α), sin(α)]) / |[Bx - Ax, By - Ay]|)


Kannst du das bitte näher erläutern?

Meinst du damit folgendes?


y= arccos(([Bx - Ax, By - Ay] * [cos(α), sin(α)]) / |[Bx - Ax, By - Ay]|)

Ansonste nmüsste ich das vom prinzip her alles hinkriegen.

---

Ja das Gleichheitszeichen hat sich da bei mir ungewollt eingeschlichen :)

Ist ja einfach der arccos vom Skalarprodukt der Vektoren durch das Produkt der Vektorlängen.