Länge eines ebenen Kurvenstücks berechnen

Question

Berechnen Sie die Länge des ebenen Kurvenstücks

x=t^6/6 , y=2-t^4/4 , t Element R+

zwischen den Schnittpunkten mit den Koordinatenachsen.

Answer 1

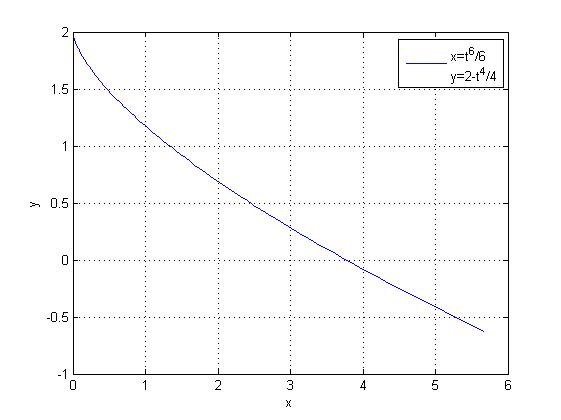
y = 0, für t = 2^{3/4}; //Insgesamt gibt es vier Lösungen, nur eine kommt in Frage da nur sie im Definitionsbereich liegt

x = 0, für t = 0; //6-fache Nullstelle; t ∈ R₀⁺ (?)

 

Formel für Längenberechnung:

L = ∫_a^b sqrt{ (y')^2 + (x')^2 } dt;

y' = -t^3;

x' = t^5;

a = 0;  b = 2^{3/4};

L = [  1/6 * (t⁴ + 1)^3/2  ]_a^b

L = 13/3;

 

lg JR

Comments

L = 1/6 * (t^4 + 1)^{3/2}+c; --> Das Ergebnis oben ist falsch

L = 13/3;

---

Ist nun ausgebessert.

---

Kann jemand noch mal die eingesetzte und umgeformte Längenformel nennen, ich sehe den Schritt zur Stammfunktion nicht.

Aus

L = ∫ab sqrt{ (y')2 + (x')2 } dt

folgt doch eigentlich durch einsetzen

L = ∫ab sqrt{ (-t^3)^2 + (t^5)^2 } dt = ∫ab sqrt{ t^6 + t^10 } dt;

 

Und davon ist die Stammfunktion doch anders, oder wo ist jetzt der Fehler?

---

erst wird Substituiert:  u = t^2;  dt = 1/(2t) du;

das führt auf 1/2 ∫u*sqrt(u^2+1)du

dann wird nochmal Substituiert: s = 1+u^2; du = 1/(2u) ds;

das führt auf 1/4 ∫sqrt(s) ds

das ist elementar Integrierbar

die Resubstitutionen vereinfachen sich, da t ∈ ℝ⁺.

 

lg JR