Wie berechne ich die Produktivität des Unternehmens?

Question

Die Produktivität [in Leistungseinheiten] eines Unternehmens, das zum Zeitpunkt t!=!0 gegründet wurde, lässt sich in Abhängigkeit von der Zeit t [in Jahren] beschreiben durch die Funktion

P(t) =30.000 / (1.800 + 2(t - 10))2

a) Mit welcher Produktivität startet das Unternehmen?
b) Nach wie vielen Jahren erreicht es seine maximale Produktivität?

Comments

Bitte den Funktionsterm einmal prüfen. Ich denke so wie er notiert ist, ist er verkehrt.

---

am ende steht hoch 2

Answer 1

Ich denke da stimmt immer noch etwas nicht

P1(t) = 30000 / (1800 + 2(t - 10))^2

P2(t) = 30 / (1.8 + 2(t - 10))^2

P1 wäre für t>0 streng monoton fallend. 

P2 würde für t = 9.1 gegen unendlich gehen.

Am sinnvollsten erscheint mir dann P2.

a) Mit welcher Produktivität startet das Unternehmen?

P2(0) = 30 / (1.8 + 2(0 - 10))^2 = 750/8281 = 0.09056877188

b) Nach wie vielen Jahren erreicht es seine maximale Produktivität?

1.8 + 2(t - 10) = 0
t = 9.1

Schau mal ob das Sinn macht.

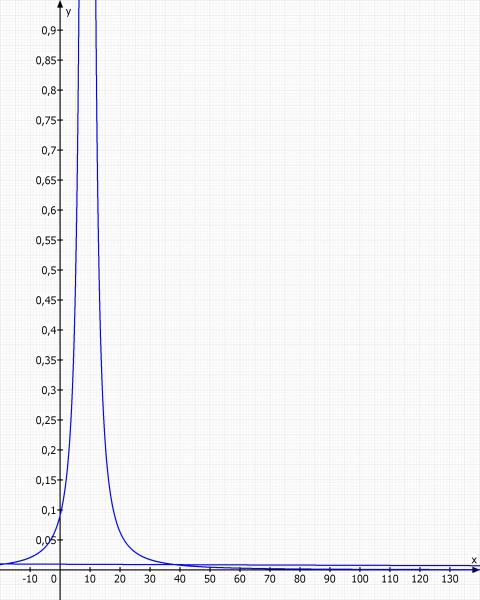
Skizze der beiden Funktionen: