Funktionsterm der Funktion, Zeichnen Sie den Graphen,Seitenlänge mithilfe der Scheitelpunktform bestimmen

Question

Von einer an einem gradlinigen Kanal gelegenen Weidefläche soll ein rechteckiges Stück unter Einschluss des Kanals als Grenze mittels eines 240 m langen Zaunes eingegrenzt werden.
a) Bestimmen Sie den Funktionsterm der Flächeninhaltsfunktion A
b) Zeichnen Sie den Graphen von A
c) Bestimmen Sie rechnerisch mithilfe der Scheitelpunktform die Seitenlängen der eingegrenzten Weidefläche so, dass der Flächeninhalt maximal ist.

Comments

Vielen Dank für die schnelle Hilfe :)

Answer 1

du hast ein Rechteck, eine Seite (b) bildet der Kanal, für drei Seiten brauchst du den Zaun

a+a+b=240 stelle nach b um b=240-2a

A(a,b)=a*b jetzt b einsetzen

A(a)=a*(240-2a)=-2a^2+240a=-2(a-60)^2+7200

Answer 2

y = Zaunstück parallel zum Kanal,  x = Zaunstücke senkrecht zum Kanal  [ Längen in Metern]

a)

2x + y = 240  →  y = 240 -2x

A(x,y) = x • y  →   A(x)  =  x • (240 - 2x)  =  240 x  - 2x²   

b)  

Die Nullstellen von A(x) sind  x=0 und x=120  

A maximal →  A'(x) = 0  ⇔  240 - 4x = 0  ⇔ x = 60   →  y = 120 

Der x-Wert des Scheitelpunkts  liegt in der Mitte  → x_s = 60 → y_s = 7200, also  S(60|7200)

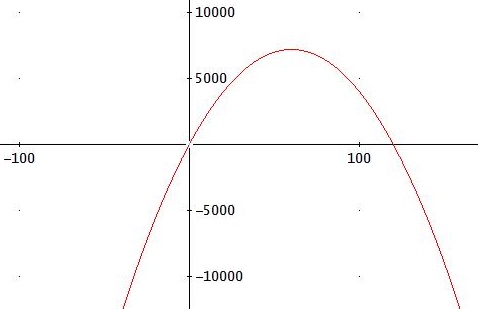
c)  Scheitelpunktform:  A(x) = - 2 • (x - 60)² + 7200

zum maximalen Flächeninhalt 7200 m ² gehören also 

die Seitenlängen  x = 60m  und y = 240 - 2x = 120m

Gruß Wolfgang

Answer 3

Hier der Graph

~plot~ -2*x²+240 * x ; [[ 0 | 100 | 0 | 8000 ]]  ~plot~

Scheitelpunkt form

-2*x²+240 * x
-2 * ( x^2 - 120 * x )
-2 * ( x^2 - 120 * x  + 60^2 - 60^2 )
-2 * ( x^2 - 120 * x  + 60^2 )  + (-2) * (-60)^2
-2 * ( x  -  60 )^2   + 7200

S ( 60  | 7200 )

In der Notation des anderen Antwortgebers

a = 60
2 * a + b = 240
b = 120