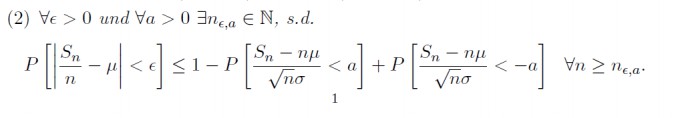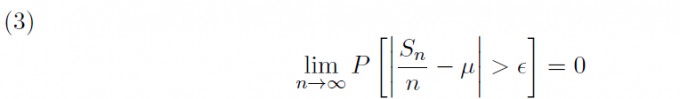Sei $${{X_k}}_{k\in\mathbb{N}}$$ eine Folge von iid Zufallsgrössen (Identisch verteilte und unabhängige Zufallsgrössen) mit $$E[X_1]=\mu$$ und $$0< v[X_1]=\sigma^2<\infty$$
Sei $$Sn=\sum_{k=1}^{n}{X_k}$$ Wir nehmen an, dass der zentrale Grenzwertsatz für alle $$a \in \mathbb{R}$$ gilt:
$$\lim_{x\to\infty}{P\left[\frac { Sn-n\mu }{ \sqrt(n)\sigma }\leq a\right]}=p[N(0,1)\leq -a]$$
Beweise folgendes, wenn n gegen unendlich geht