Wie komme ich auf auf diese Beschränktheit?

Question

 

ich weiß leider nicht, wie ich meine Frage formulieren soll. 

In der Vorlesung wurde folgendes vorgerechnet und ich habe keine Ahnung, wie man auf so etwas kommt. 

Hier die Aufgabe:

(a_n ) ist beschränkt. Es gilt:

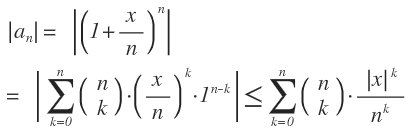
Hier schon mal meine erste Frage.

1.  Wie kommt er auf diese Ungleichung? Gibt es dazu einen Satz?

1.1 Warum kann ich das x im Betrag lassen? 

1.2 Wie komm ich denn darauf, dass ich genau x im Betrag lassen muss?

So nun hat der Professor zunächst einmal etwas anderes gezeigt und das dann in der Rechnung angewendet:

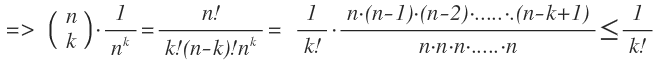
Meine Frage: 

2. Wenn man abschätzt, darf ich da nur etwas "wegfallen" lassen oder auch etwas neues hinzufügen?

Nun weiter zur Aufgabe :

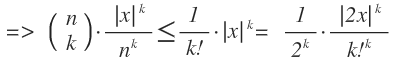
So das hier ist mein größtes Problem. 

3.1 Wie komme ich hier auf dieses Endergebnis, Woher kommen auf einmal die (1/2^k) her.

3.2 Warum wurde aus ΙxΙ^k =>  Ι2xΙ^k 

3.3 Woher kommen die k!^k ? 

Die Aufgabe geht zwar noch weiter, aber ich verstehe die einzelnen Schritte nicht. Eine Lösung der ganzen Aufgabe brauche ich nicht. Nur die Erklärung für diese Schritte :/

Vielen vielen vielen Dank schon einmal für die Antworten. Ich weiß, es sind recht viele Fragen, aber ich hoffe jemand kann sie mir beantworten. :)

Schönen Sonntag euch.

Answer 1

1) Es wurde die Dreiecksungleichung verwendet.

1.1) Du kannst nicht nur, du musst sogar.

1.2) Alle anderen Faktoren sind positiv, so dass man die Beträge an diesen Stellen weglassen kann.

2) Das ist so vage gestellt, dass ich dir nur so antworten kann: Beim Abschätzen darfst du alles machen, so lange die Abschätzung korrekt ist.

3.1) Der Bruch wurde mit \(2^k\) erweitert.

3.2) \(2^k \cdot |x|^k = |2|^k \cdot |x|^k =  |2x|^k \).

3.3) Gute Frage, die Potenz ist hier total fehl am Platz und das Gleichheitszeichen somit falsch.

Gruß

Comments

:)

Ich habe aber eine dennoch eine Frage....

Was meinst du mit " Es wurde die Dreicksungleichung verwendet"?

Ich kenne nur das hier:

Ιx+yΙ ≤ ΙxΙ +ΙyΙ

und Ιx-yΙ ≥ ΙxΙ -ΙyΙ. 

Ich habe noch nie die Dreiecksungleichung beim Summenzeichen verwendet o.O

---

Kein Thema, für Rückfragen stehe ich gerne zur Verfügung :).

Es ist schon mal gut, dass du die Dreiecksungleichung kennst. Induktiv kann man sie natürlich noch weiter verallgemeinern (sehr wichtig für das weitere Studium). Für \(n \in \mathbb{N}\) seien \(x_i \in \mathbb{R} \), wobei \(1 \leq i \leq n\). Dann gilt:

$$ | x_1 + x_2 + \dots + x_n | \leq |x_1| + |x_2| + \dots + |x_n| $$

oder kürzer notiert:

$$\left | \sum_{i=1}^n x_i \right | \leq \sum_{i=1}^n|x_i| $$