Funktionenschar mit f_(k)(x): = 2x^2 - 3kx^2 + k^3, k€R. Berührung der x-Achse und Beziehung f_(k) und f_(-k)?

Question

Ich brauche unbedingt die Rechnung 

Comments

Es wäre schön, wenn du dich bei den Antworten zu deinen vielen Fragen, kurz bedanken würdest. (Auch Daumen und Sterne darfst du vergeben). So hat man den Eindruck, dass die Mühe auch geschätzt wird und dir weiterhilft. 

Answer 1

a)
1. Ableitung
f'(x)=6*x^2-6*k*x
0=6*x^2-6*k*x
0=x^2-k*x
0=x*(x-k)

für x=k wird der Faktor (x-k)=0, somit liegt an der Stelle x=k ein Extrempunkt vor

f(k)=2*k^3-3*k^3+k^3
f(k)=0 somit liegt der Extrempunkt auf der x-Achse

b)


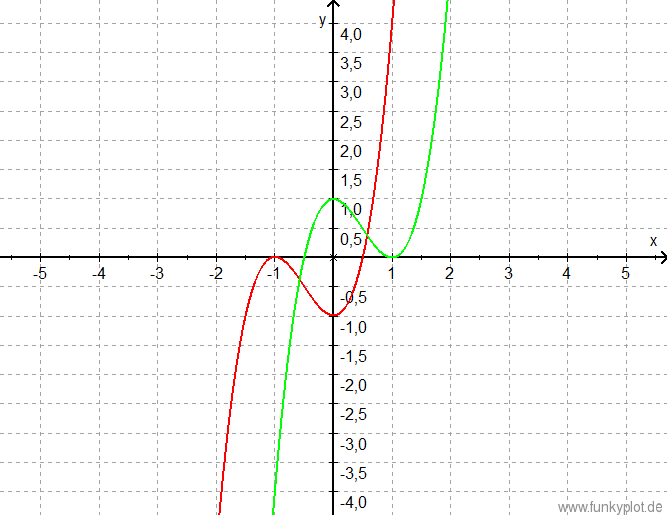
rot: k=-1
grün: k=1

c)
ich gebe dir als Srichwort "Symmetrie" mit