Bestimmung des Definitonbereiches von arccos(sqrt(1/x))

Question

ich komme beim Bestimmen des Definitionsbereiches folgender Aufgabe nicht weiter:

 

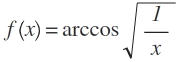
Mein Ansatz:

Es muss bei einer arccos-Funktion gelten:

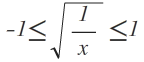
Also 1. Fall :

 

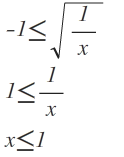
Daraus folgt:

Lösungsmenge₁= ]−∞;1]

2. Fall:

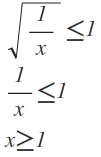
 Daraus folgt:

Lösungsmenge₂= [1;+∞[

x darf aber keinen Wert ≤0 annehmen, wegen dem Bruch und der Wurzel

Also ist mein Ergebnis: L=]0;1]∩[1;+∞[

Leider ist das falsch, die richtige Lösung lautet nähmlich: ]1;+∞[

Ich vermute den Fehler beim Lösen der Ungleichungen, weiß aber nicht wo dieser liegt...

Würde mich sehr freuen, wenn Ihr mir weiterhelfen könntet

Answer 1

Wurzeln sind nichtnegative Zahlen.

√(1/x)  kann nicht kleiner als 0 sein. 

Zudem muss von Anfang an gelten x > 0. 

Nun kannst du die cos-Bedingung noch einbeziehen in die Rechnung.

"die richtige Lösung lautet nämlich: ]1;+∞[ "

Warum ist da 1 nicht dabei? [ 1;+∞[ wäre logischer. 

Comments

Dass x>0 ist hab ich doch in "x darf aber keinen Wert ≤0 annehmen" genannt.
Null darf aber auch nicht angenommen werden, da sonst Null in Nenner stehen würde, was nicht definiert ist. Mir ist nicht ganz klar, was es an meinerm Ergebnis ändern würde, wenn ich bereits zu Anfang von x>0 ausgehen würde.
Die Lösung ]1;+∞[ ist zu 100% so richtig.
Und nämlich mit h ---> fail :/

---

https://www.wolframalpha.com/input/?i=arccos%281%29+

arccos(1) = arccos( √(1/1)) ist definitiv möglich. 0 ist schliesslich auch eine Zahl. 

Also: 

] 0 ;+∞[  n  [ 1,+∞[  = [ 1,+∞[

Zudem: Aha. Ich hatte deine Antwort nicht ganz gelesen und dachte, du wolltest da noch negative x-Werte dazunehmen. Du hast da aber: 

]0;1]. Das widerspricht dem 1/x ≤ 1. Ausser gerade bei x = 1. 

---

Prüfe deine Umformung

- 1 ≤ √(1/x)

1 ≤ 1/x

mit

- 1 ≤ √(1/2)

1 ≤ 1/2        ? 

- 1 ≤ √(1/x)

1 ≤ 1/x       geht also nicht. 

---

Du hast recht, die erste Ableitung ist definiert mit ]1;+∞[. Ich hab' fälschlicherweise angenommen, dass das auch für die Ausgangsfunktion gilt! Dass meine Umformung falsch ist, hatte ich ja bereits angenommen. Aber leider sehe ich meinen Fehler nicht... Hab auch schon im Internet nach Ungleichungen in Kombination mit Wurzeln gesucht, finde aber keine zielführenden Ergebnisse. Muss ich nach dem quadrieren von -1≤√1/x eine Fallunterscheidung machen?

---

Quadrieren ist in deinem Fall eine Multiplikation mit einer negativen Zahl. 

Sollte man das je machen, ändert sich das Ungleichheitszeichen.

Aber du solltest besser von Anfang an nur

0 ≤ √(1/x) ≤ 1 ansehen und x > 0.