funktion verschieben x⁴ - 17x² + 16 nach oben

Question

f(x)= (x+1) (x-1) (x+4) (x-4)

um wie viele einheiten muss man die funktion mindestens nach obrn verschieben, so dass sie keine nullstelle mehr hat?

es sind so ca. 56,25 aber wie kommt man darauf??

Answer 1

f(x) =   x⁴ - 17x² + 16     →  g(x) = x⁴ - 17x² + a     

x⁴ - 17x² + a = 0

Setze z=x²

pq-Formel:

z² - 17z + a = 0

z_1,2 = - 17/2 ± √ [ (-17/2)² - a]    für (-17/2)² - a ≥0   [sonst keine Nullstellen weil Radikand negativ]

a ≤ 289/4 

289/4 -16 = 56,25

Die Funktion  f(x) = x⁴ - 17x² + 16 muss also um mehr als  56,25 nach oben verschoben werden.

 

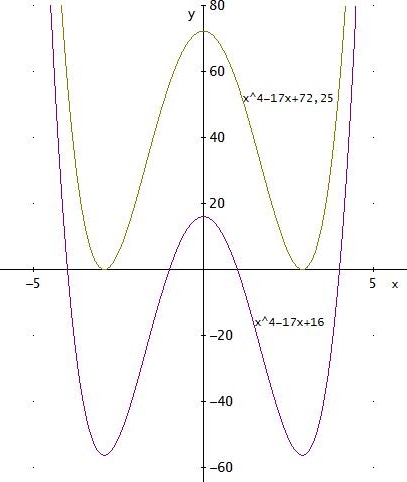
Bei den Funktionsgleichungen im beim Graph muss es "-17x²" heißen

Gruß Wolfgang

Answer 2

f ( x ) = x^4 - 17 * x^2 + 16

g ( x ) = x^4 - 17  * x
Hoch- und Tiefpunkte ermitteln
g ´( x ) = 4 * x^3 - 34 * x

4 * x^3 - 34 * x = 0
x * ( 4 * x^2 - 34 ) = 0
x = 0
und
4*x^2 - 34 = 0
4x^2 =  34
x^2 = 8.5
x = 2.915
f ( √ 8.5 ) = 8.5^2 - 17 * 8,5 = -72.25
T ( √ 8.5  | -72.25 )
Weiter wie bei Wolfgang

Der Rechenweg ist zwar etwas langwieriger
aber zum einmal Aufzeigen auch sicher interessant.

Comments

Er hat auch den Vorteil, dass man es so machen kann, wenn die Gleichung für die Nullstellen nicht so schön "passt" :-)