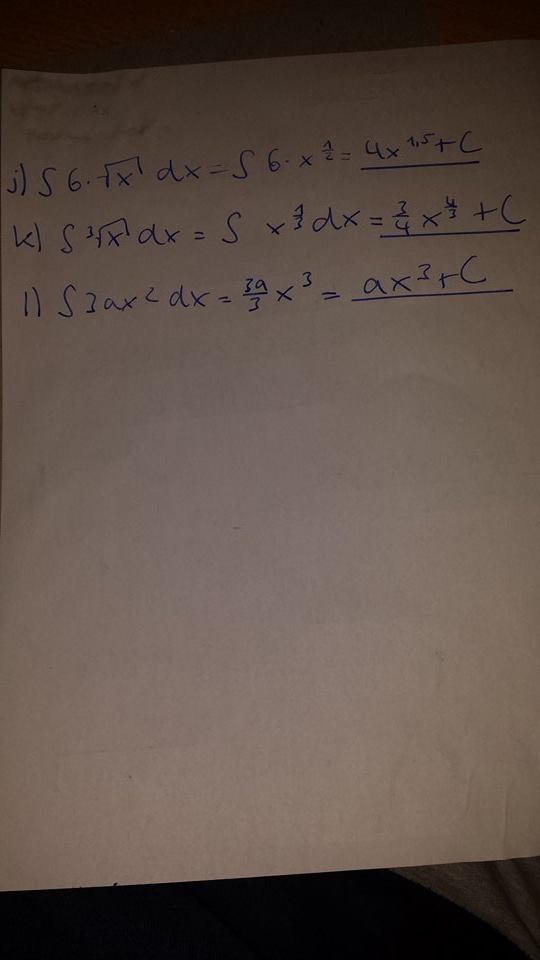Aufgabe 3.
Kann jemand sich bitte alle Lösungen zu dieser Aufgabe anschauen... Außerdem komme ich bei c) und g) auf zwei verschiedene Lösungen...
Berechnung unbestimmter Integrale
a) \( \int x^{6} d x \) b) \( \int 6 x^{2} d x \) c) \( \int n \cdot x^{2 n-1} d x \) d) \( \int\left(4 x^{2}+2 x\right) d x \)
e) \( \int\left(2 x^{3}-4 x+1\right) d x \) f) \( \int\left(a x^{2}+6 x\right) d x \) g) \( \int 3 x^{-2} d x \) h)\( \int\left(2 x+\frac{1}{x}\right) \cdot x\, d x \)
$$
\]
i) \( \int\left(x+\frac{3}{x^{2}}\right) d x \) j) \( \int 6 \cdot \sqrt{x} d x \) k) \(\int \sqrt[3]{x}\, dx \) l)\( \int 3 a x^{2} d x \)