Nullstelle, Extremstelle, auf welchen Intervallen ist f streng monoton wachsend/fallend?

Question

gegeben ist die Funktion f(x) = sin(cos(x)), welche durch f : ℝ→ℝ definiert ist.

Ich komme nicht mehr weiter und brauche Hilfe bei der Bestimmung von:

1.) Nullstellen

2.) Extremstellen

3.) Auf welchen Intervallen ist f streng monoton wachsend bzw. fallend?

Wäre nett, wenn mir einer Helfen könnte, gerne auch mit Lösungsweg.

Answer 1

f(x) = sin(cos(x))    D = ℝ

Nullstellen:

sin(cos(x) = 0

Sinus hat die Nullstellen k • π mit k∈ℤ

⇔  cos(x) = k • π   mit k∈ℤ

⇔ cos(x) = 0     [ weil -1 ≤ cos(x) ≤ 1 ]

⇔  x = π/2 + k • π  mit k∈ℤ

Extremwerte:

f'(x) = -sin(x) • cos(cos(x))

⇔  sin(x) = 0  oder cos(cos(x))  = 0

⇔  x = k•π  oder cos(x) =  π/2 + k • π  

Letzteres hat keine Lösung  wegen  -1 ≤ cos(x) ≤ 1

⇔  x = k • π    k∈ℤ 

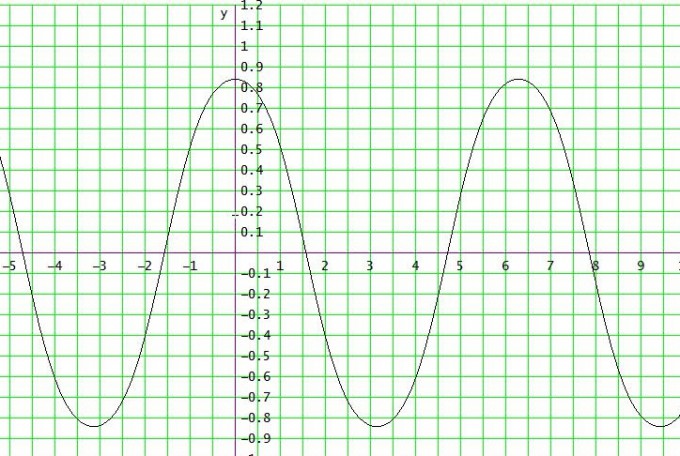
Also:  H ( 2k • π |  sin(1) )  ≈ ( 2k • π |  0,841 )    ,   T ( (2k+1) • π  | - sin(1) )

Monotonieintervalle  (k∈ℤ) :

[ k•π ; (k+1)•π ]  streng monoton fallend

[ (k-1)•π ; k•π ]  streng monoton steigend

Gruß Wolfgang

Answer 2

1. cosx = 0 

x = pi/2  oder x= (3/2)*pi

2.

f '(x) = cos(cosx)*(-sinx)

cos(cosx) = 0

x= ...

oder:

-sinx = 0

x= ...