Integralrechnung mit Steckbriefaufgaben. Im Ursprung ein Wendepunkt ...

Question

Hallo liebe Leute,ich hab mich aus Verzweiflung hier angemeldet. Ich kam eigentlich immer relativ gut zurecht, aber jetzt kommen aufgeben wo ich nicht weiter weiss.
1.Eine ganzrationale Funktion 4. Grades schneidet die X-Achse bei x=4 und hat im Ursrpung einen Wendepunkt mit waagerechter Tangente. Sie schließt mit der X-Achse im 1. Quadranten eine Fläche von 6,4 F.E. ein. Wie lautet die Funktion ?
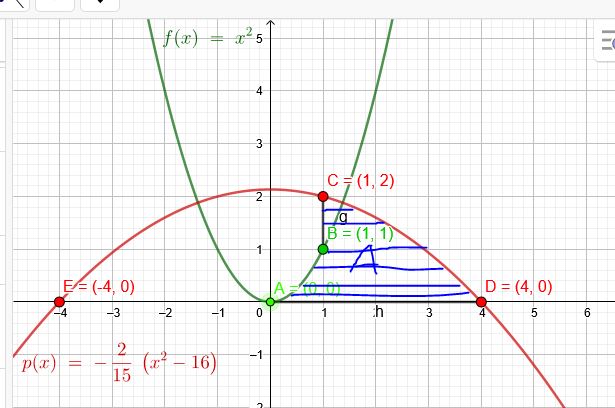
2.Eine achsensymmetrische Parabel verläuft durch A(0/0) und B(1/1). Eine andere achsensymmetrische Parabel geht durch C(1/2) und D(4/0). Berechne die Fläche, die von den beiden Parabeln sowie den Strecken BC und AD begrenzt wird.

Ich wäre euch sehr dankbar, wenn ihr mir eventuell sagen könntet wie ich an die Aufgaben rangehen soll. Wo ich das nachlesen kann oder welche Themen das genau sind. Ich suche seit einer Stunde aber kann kaum was finden, hab hier bisschen was versucht, aber kriege es nicht hin. mfG Patrick :-)

Answer 1

zu 1)

Die Funktionsgleichung einer ganzrationalen Funktion 4. Grades lautet:
f(x)= ax⁴+bx³+cx²+dx+e
Mit den restlichen Angaben lassen sich die gesuchten Koeffizienten a, b, c, d und e bestimmen.

Gegeben ist:
a) f(4) = 0 (Nullstelle bei x=4)
b) f(0) = 0 (f verläuft durch den Ursprung, d.h. weitere Nullstelle bei x=0)
c) f´´(0) = 0 (Wendepunkt bei x=0)
d) f´(0) = 0 (Waagrechte Tangente im Ursprung)
e) Wert des Integrals von einer zur anderen Nullstelle im 1. Quadrant beträgt 6,4.

Comments

Vielen Dank für die schnelle Antwort ! :-)

Das mit 1 hab ich jetzt verstanden, fehlt nur noch 2 :-)

---

zu 2)

Gleichung der ersten achsensymmetrischen Parabel:
f(x) = ax²+b
Gleichung der zweiten achsensymmetrischen Parabel:

g(x) = cx²+d

Mit den restlichen Angaben lassen sich die gesuchten Koeffizienten a, b, c und d bestimmen.
Im Anschluss daran kann die Fläche betrachtet werden.

Gegeben ist:
a) f(0)=0
b) f(1)=1
c) g(1)=2
d) g(4)=0

---

Vielen Dank !! Ich habe beide Antworten komplett verstanden, danke !