Stochastik: Ein Spielfeld mit 6x8 Punkten, die es in 6 verschiedenen Farben...

Question

ich brauche einmal Hilfe bei folgender Aufgabenstellung:

Es gibt ein Spielfeld mit 6x8 Punkten. Die Punkte sind in 6 verschiedenen Farben vorhanden.

Wie hoch ist die Wahrscheinlichkeit, dass weniger als drei gleichfarbige Punkte nebeneinander sind?

Ich war leider nie ein Mathegenie und der Unterricht ist schon eine Weile her, also Ideen wären super... :)

Comments

den einzigsten Tipp den ich geben kann ist über die Gegenwahrscheinlichkeit zu rechnen das genau drei gleichfarbige Kugeln nebeneinander liegen

Answer 1

Skizze:

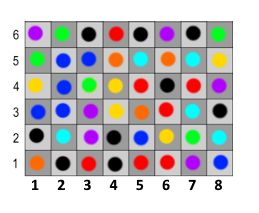
Was sehen wir hier? Es liegen hier nicht 3 gleichfarbige Punkte nebeneinander. Die Wahrscheinlichkeit dafür scheint also niedrig zu sein.

Nebeneinander heißt von links nach rechts. Wie hoch ist die Wahrscheinlichkeit, dass 3 gleichfarbige Punkte nebeneinander sind? Weil es 8 verschiedene Farben gibt, beträgt sie (1/8)^3.

Und nun müssen wir nur noch schauen, wie wir das mit den 6x8 Feldern am besten ausrechnen. Es können ja entweder die ersten 3 Felder die gleiche Farbe haben oder das zweite, dritte und vierte Feld, und so weiter:

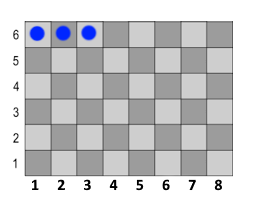oder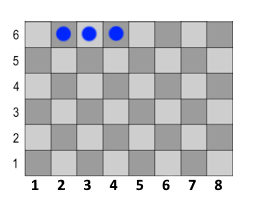

Pro Reihe gibt es 6 Möglichkeiten und dadurch gibt es bei unserem 6x8 Spielfeld insgesamt 6 * 8= 48 mögliche Tripletts. Diese Anzahl müssen wir nur noch mit der Einzelwahrscheinlichkeit multiplizieren also: 48 * (1/8)^3 = 0.09375.

Um jetzt auszurechnen, wie groß die Wahrscheinlichkeit ist, dass weniger als drei gleichfarbige Punkte nebeneinander sind, müssen wir diese Zahl nur noch von 1 subtrahieren, also 1 - 0.09375 = 0.90625 = 90.6%.

Ungefähr bei jedem 10-ten Spiel liegen mindestens 3 gleichfarbige Punkte nebeneinander.

Comments

Diese Antwort enthält mehrere Fehler.