Stadion mit 400-m-Laufbahn soll möglichst grosses Fussballfeld enthalten.

Question

Aufgabe:

Ein Sportstadion mit einer 400-m-Laufbahn soll so angelegt werden, dass das Fußballfeld möglichst groß ist. Die beiden Kurven sollen Halbkreise sein. Bestimme, für welche Länge und für weiche Breite das Fußballfeld maximal Wird. Wie groß ist es?

Ansatz:

Ich habe jetzt eine Gleichung aufgestellt:

U(Station)= 2πr+2a
400 m= 2πr+2a

Aber da ich hier zwei Unbekannte habe, weiß ich nicht wie ich das weiter berechnen.

Comments

Vom Duplikat:

Titel: Quadratische Extremalprobleme

Stichworte: extremalproblem,extremalwertaufgabe,maximal

Aufgabe:

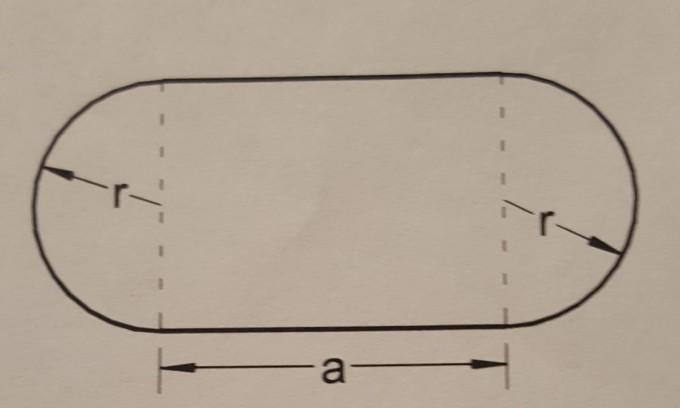
Eine 400m Bahn soll so angelegt werden, dass die Fläche innerhalb der Bahn maximal wird. Wie groß ist der Bahnradius r, die geraden Strecken a und die maximale Innenfläche der Bahn?

Problem/Ansatz:

Ich habe komische Werte bekommen.400 für den Radius und -1056.63706 für a.

Ich habe es so berechnet: 400 = 2*r*pi + 2*a

a = 400-2*r*pi/2

400 = 2*r*pi+2*(400-2*r*pi/2) => r = 400, a = -1056.63705

Das macht keinen Sinn, oder?

Könnte mir jemand helfen?

---

Vom Duplikat:

Titel: Wie berechnet man das? Extremwertprobleme

Stichworte: extremwertproblem,extremwertaufgabe

Aufgabe:

Ein Sportstadion mit einer Laufbahn mit 400m Länge soll so angelegt werden, dass

die Fläche A des eingeschlossenen Rechtecks als Fußballfeld möglichst groß

wird.

Wie berechnet man das?

---

Hallo, die Frage wurde hier schon einmal beantwortet:

https://www.mathelounge.de/321198/stadion-laufbahn-moglichst-grosses-fussballfeld-enthalten

Answer 1

Eine Extremwertaufgabe

U = 400 m = 2 * a + 2 * r * π
( 2 mal die Gerade und ein Kreis )
200 = a + r * π
a = 200 -r * π

Fläche
A = a * 2 * r
A ( r ) =  ( 200 -r * π) * 2 * r
A ( r ) = 400 * r - 2 * r^2 * π
1.Ableitung bilden
A ´ ( r ) = 400 - 4 * r *π
zu Null setzen
400 - 4 * r *π = 0
r = 100 / π

Alle Angaben ohne Gewähr.
Bin bei Bedarf gern weiter behilflich.

Comments

Warum haben Sie A=2a*r geschrieben? Ich hätte nur A=a*r geschrieben.

---

R ist nur der Radius ( Halbmesser )

Die Breite ist 2 * r.
Die Fläche ist Länge mal Breite also
A = a * ( 2 * r )

Answer 2

Breite des Fußballfeldes 2r; Länge des Fußballfeldes b. Dann ist 2πr+2b=400 und b = 200-πr. Zu maximieren ist f(r)= b·2r. Für b einsetzen f(r)=(200-πr)·2r. Das ist die Gleichung einer quadratischen Parabel. Der Rest ist einfach

Answer 3

Stadion Aufgabe

 

Comments

a=100 ist falsch. Den Fehler hatte ich auch gemacht. Wir müssen nicht nach a, sondern nach r die Ableitung machen.

A ergibt dann ca. 10 000 m2

---

a=100 ist falsch. Den Fehler hatte ich auch gemacht. Wir müssen nicht nach a, sondern nach r die Ableitung machen.

Die Lösung ist in jedem Fall$$a = 100\,\text m, \quad r = \frac{100}{\pi}\,\text m$$Du kannst die Nebenbedingung auch nach \(a\) auflösen, in die Hauptbedingung einsetzen und dann nach \(r\) ableiten. $$A=2ar \to \max \\ \begin{aligned}2\pi r + 2a &= 400 \\ a &= \frac {400}2 - \pi r \end{aligned}\\ A=2\left(\frac {400}2 - \pi r\right)r = 400r - 2\pi r^2 \\ \frac{\partial A}{\partial r} = 400-4\pi r \to 0 \\ \implies r = \frac{100}{\pi}$$Das ändert aber nichts an der Lösung.

A ergibt dann ca. 10 000 m²

das wäre ein Quadrat mit der Kantenlänge von \(100\,\text m\) und einem Umfang von \(400\,\text m\). Aber dann hätte die Laufbahn keine Kurven!

---

ach stimmt, hast Recht

---

dein r ist da auch richtig, aber a kann so nicht stimmen:
2r=b

Ich unterstelle, dass \(b\) die 'Höhe' des Ovals oben im Bild ist.

und b=a also ein Quadrat ergibt bei einem Rechteck immer den größten Inhalt bei kleinstem Umfang.

das ist richtig, aber löst nicht dieses Problem! Hier ist nicht der Umfang des Rechtecks konstant, sondern der Umfang des Ovals. Und dort gehen die 'Seiten' mit dem Faktor \(\pi/2\) ein. Der Umfang \(U\) ist$$U = 2a + 2b \cdot \frac \pi2$$Am Ende ist der Inhalt des Rechtecks dann wieder maximal groß, wenn man den Umfang in 4 gleichen Teilen auf die 4 Seiten verteilt. Nur sind eben hier zwei der Seiten 'rund'!

---

danke     :)

Answer 4

Hi,

1. Formel für den Umfang aufstellen (2 Geraden, 2 Halbkreise).

2. Nach a oder r auflösen, je nach Gusto.

3. In die Flächenformel für des rechteckige Fussbalfeld einsetzen.

4. Von der quadratischen Funktion aus 3. den Scheitelpunkt bestimmen.