Funktionsgleichung der Brückenkonstruktion mit Hilfe der Nullstellen berechnen

Question

Ich brauche bei meiner letzten Aufgabe Hilfe:

Ich habe Aufgabe 3b und c grafisch gelöst:

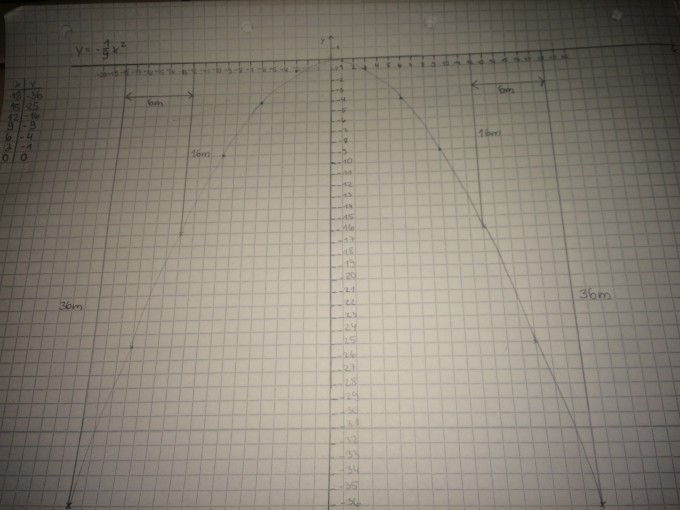
Nun komme ich aber bei Aufgabe 3d absolut nicht mehr weiter.

Als Gleichung habe ich y=-1/9x² gegeben. Laut Aufgabe d soll die x-Achse nun unterhalb des sichtbaren Bogens verlaufen. Dann hätte ich ja die Nullstellen x₁= -18 und x₂=18 und den Extremwert (0|36). Laut Aufgabe soll ich die Funktionsgleichung aufstellen. Nur habe ich keine Ahnung wie ich das angehen soll. Ich hab zwar Lösungen für Gleichungen der Form y=ax²+bx+c gefunden, doch ich habe ja nur eine Gleichung der Form ax², oder? Also wie kann ich bei der Form die Funktionsgleichung aufstellen?

Liebe Grüße und !

Answer 1

Hallo Regenbogenelfe,

die rechnerische Lösung:

b) \(f(18) = -36 \)

Die langen Stützen sind 36 m lang.

c) \(f(12) = -16 \)

Die kurzen Stützen sind 16 m lang.

d) Du musst die Parabel im Koordinatensystem einfach nur um die Länge der langen Stütze nach oben verschieben.

Neue Funktion: \(g(x) = -\frac{1}{9}x^2 + 36 \).

Gruß

Comments

Danke dir! Eigentlich ist das so einfach, dass ich auch selbst hätte drauf kommen können, aber ich stand wohl auf der Leitung. Danke auch noch mal für die Veranschaulichung von Aufgabe b und c, da weiß ich, dass meine Zeichnung so auch stimmt.

Answer 2

Sicherlich ist folgendes gemeint :
du gehst oben bis zum Scheitelpunkt der Parabel.
Dann 2 Stützen nach links oder rechts.
Diese Stützen versinken unten im Erdreich
( l ist die Länge oder h die Höhe der Stützen )
Zwischen diesen beiden Punkten wird die neue x-Achse gelegt.
Die Funktionsgleichung heißt nun
g ( x ) = f ( x ) + h = -1/9 * x^2 + h
( h ist  nunmehr der y-Achsenabschnitt )

Der Parabelbogen wird in Richtung y-Achse dadurch nach oben
geschoben weil die x-Achse nunmehr woanders ist.