die Gerade h durch P, die auf g senkrecht steht, hat den Richtungsvektor \(\vec{u}\) = \( \begin{pmatrix} -2 \\ 1 \end{pmatrix}\) (Skalarprodukt mit dem Richtungsvektor von g = 0)
Eine Parameterform ist also: h: \(\vec{x}\) = \(\begin{pmatrix} 3 \\ 4 \end{pmatrix}\) + r • \( \begin{pmatrix} -2 \\ 1 \end{pmatrix}\)
Der Schnittpunkt L von g und h ergibt sich aus
\( \begin{pmatrix} 3 \\ 4 \end{pmatrix}\) + r • \( \begin{pmatrix} -2 \\ 1 \end{pmatrix}\) = \( \begin{pmatrix} 5 \\ 3 \end{pmatrix}\) + k • \( \begin{pmatrix} 1 \\ 2 \end{pmatrix}\)
→ k + 2r = -2 und 2k - r = 1 → k = 0 und r = -1 → L(5|3)
Der Spiegelpunkt P ' von P an g hat den Ortsvektor \(\overrightarrow{OP'}\) = \(\overrightarrow{OL}\) + \(\overrightarrow{PL}\)
→ \(\overrightarrow{OP'}\) = \( \begin{pmatrix} 5 \\ 3 \end{pmatrix}\) + \( \begin{pmatrix} 2 \\ -1 \end{pmatrix}\) = \( \begin{pmatrix} 5 \\ 5 \end{pmatrix}\)
→ Spiegelpunkt P ' (7 | 2)
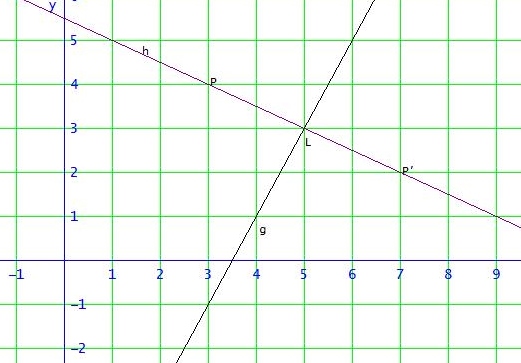
Man könnte hier in der Ebene natürlich auch mit Geradengleichungen der Form y = mx + n rechnen.Die oben angewendete Vektorrechnung hat aber den Vorteil, dass sie sich problemlos auf Geraden im Raum erweitern lässt.
Gruß Wolfgang