Polynomfunktion vierten Grades

Question

ich stecke hier fest,

Sattelpunkt (0/0) und Wendepunkt (1/1)

Stimmt das?

f (0)=0

f (1)=1

f '' (1)=0 -> 2 ableitung wedepunkt

f '' (0)=0 -> 1 ableitung sattel

f '' (0)=0 -> 2 ableitung sattel

kommt leider was falsches heraus.

richtig wäre: -x⁴+2x³

Comments

4. Zeile muss heissen:

f '' (0)=0 -> 1 ableitung sattel 

muss heissen

f ' (0)=0 -> 1 ableitung sattel 

Answer 1

Hi,

das ist alles richtig, wenn man in der vorletzten Zeile einen Schreibfehler annimmt. Da sprichst Du von der ersten Ableitung, schreibst aber die zweite hin ;).

f(0) = 0

f'(0) = 0

f''(0) = 0

f(1) = 1

f'(1) = 0

Und das führt dann schnell auf:

f(x) = -3·x^4 + 4·x^3

Alles klar?

Grüße

Comments

Bei mir kommt dann -> nicht genug variablen

habe es genau so gemacht.

---

Wo kommt das?

Hier ergibt sich doch sofort c = d = e = 0

Dann haste noch die letzten beiden Zeilen, welche, wenn man die obigen einsetzt, so aussehen:

a + b = 1

4a + 3b = 0

Das dann halt noch ausrechnen (ersteres nach a auflösen und in letzteres einsetzen oder anderes)

---

Ich habe es mit Mathematics gemacht, dass ist ein Programm.

Habe es jetzt vollständig. Herzlichen Dank!

---

Die Funktion hat ein Maximum bei x=1. Es soll dort aber ein Wendepunkt sein.

---

Richtig, da bin ich damals wohl mit der ersten/zweiten Ableitung durcheinander gekommen:

MIt:

f(0) = 0
f'(0) = 0
f''(0) = 0
f(1) = 1
f''(1) = 0

--> f(x) = -x⁴ + 2x³

Merci

Answer 2

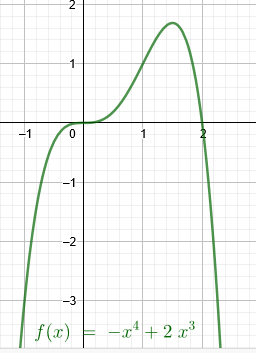
Sattelpunkt (0|0) und Wendepunkt W(1|1)  4.Grad

f(x)=a*\( x^{3} \) (x-N)

W(1|1)

f(x)=a(1-N)

1.) a(1-N)=1      a=\( \frac{1}{1-N} \)

f(x)=\( \frac{1}{1-N} \)*[\( x^{3} \)(x-N)]=\( \frac{1}{1-N} \)*[\( x^{4} \)-\( x^{3} \)N]

f´(x)=\( \frac{1}{1-N} \)*[4\( x^{3} \)-3\( x^{2} \)N]

f´´(x)=\( \frac{1}{1-N} \)*[12\( x^{2} \)-6xN]

f´´(1)=\( \frac{1}{1-N} \)*[12-6N]

\( \frac{1}{1-N} \)*[12-6N]=0    N=2    a=-1

f(x)=-\( x^{3} \) (x-2)=-x^4+2x^3