Suche optimale Losgrösse. f(x)= 12500:x + 5x:100

Question

Ich habe folgende Gleichung, bei dessen Lösung ich nicht weiterkomme:

opt. Losgrösse \( =\frac{12500}{x}+\frac{5 x}{100} \)

Es handelt sich um eine Alternative zur Andler'schen Losgrößenformel und soll so aufgelöst werden, dass am Ende ein X-Wert (Lösung müsste ~500 Stück sein) rauskommt.

Answer 1

Annahme: Du brauchst eine Extremalstelle deiner Funktion.

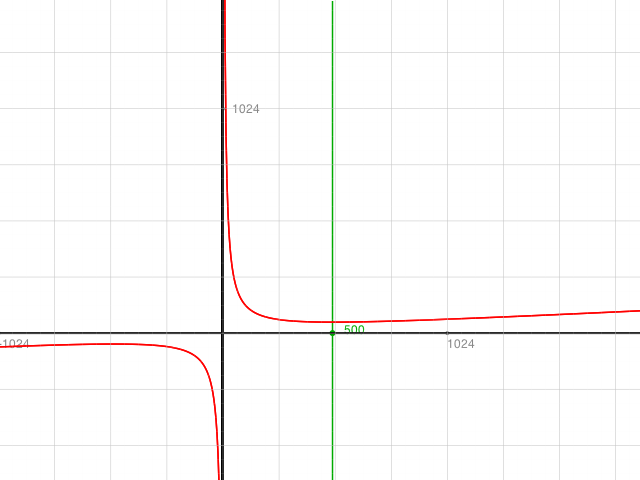
Gemäss Skizze wäre bei etwa 500 ein lokales Minimum zu erwarten.

f(x)=12500:x + 5x:100

 = 12'500x^{-1} + x/20

Erste Ableitung = 0 setzen und schrittweise nach x auflösen.

f ' (x) = -12'500 x^{-2} + 1/20 = 0         |+12'500 x^{-2}

1/20 = 12'500 x^{-2}          |*x^2; * 20

x^2 = 20*12'500

x^2 = 250'000         |±√

x = ±500

Aus Plausibilitätsgründen kommt wahrscheinlich nur die positive Lösung als x-Wert in Frage.