Ich verstehe die b) nicht... :)
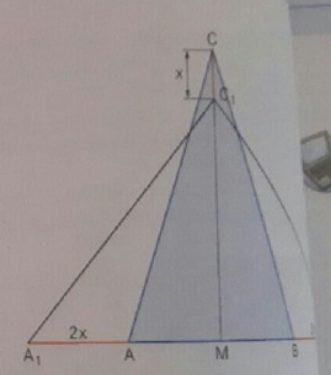
Grgeben ist ein gleichschenkliges Dreieck ABC mit der Grundseitenlänge \( \overline{A B}=5 \mathrm{cm} \) und der Höhe \( \mathrm{h}=\mathrm{MC}=8 \mathrm{cm} . \) Es entstehen neue Dreiecke \( A_{n} B_{n} C_{n}, \) wenn man die Seite \( |A B| \) über \( A \) und \( B \) hinaus je um \( 2 x \) cm verlängert und gleichzeitig die Höhe h von C aus um \( \mathrm{x} \) cm verkürzt.
a) Zeichne das Dreieck ABC und ein neues Dreieck \( A_{1} B_{1} C_{1}, \) für \( x=2 \) und berechne seinen Flächeninhalt \( A_{1} \).
b) Welche Werte kann x annehmen?
c) Bestimme den Flächeninhalt A der Dreiecke \( A_{n} B_{n} C_{n} \) in Abhängigkeit von \( x \). [Ergebnis: \( \left.A=\left(-2 x^{2}+13,5 x+20\right) \mathrm{cm}^{2}\right] \)